Csdrhrt

En matemática, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula(A,B..) y sus elementos con la misma letra en minúscula (a,b...), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece.

A=(a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn){displaystyle mathbf {A} ={begin{pmatrix}a_{11}&a_{12}&cdots &a_{1n}\a_{21}&a_{22}&cdots &a_{2n}\vdots &vdots &ddots &vdots \a_{m1}&a_{m2}&cdots &a_{mn}\end{pmatrix}}}

Los elementos individuales de una matriz m{displaystyle m} x n{displaystyle n}, a menudo denotados por ai{displaystyle a_{i}}y aj{displaystyle a_{j}}, donde el máximo valor de sus elementos (i{displaystyle i}, j{displaystyle j}) en i{displaystyle i} es m{displaystyle m}, y el máximo valor de j{displaystyle j} es n{displaystyle n}. Siempre que la matriz tenga el mismo número de filas y de columnas que otra matriz, estas se pueden sumar o restar elemento por elemento.

Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar transformaciones lineales dada una base. En este último caso, las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.

Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.

Historia

El origen de las matrices es muy antiguo. Los cuadrados latinos y los cuadrados mágicos se estudiaron desde hace mucho tiempo. Un cuadrado mágico, 3 por 3, se registra en la literatura china hacia el 650 a. C.^[2]​

Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un importante texto matemático chino que proviene del año 300 a. C. a 200 a. C., Nueve capítulos sobre el Arte de las matemáticas (Jiu Zhang Suan Shu), es el primer ejemplo conocido de uso del método de matrices para resolver un sistema de ecuaciones simultáneas.^[3]​ En el capítulo séptimo, "Ni mucho ni poco", el concepto de determinante apareció por primera vez, dos mil años antes de su publicación por el matemático japonés Seki Kōwa en 1683 y el matemático alemán Gottfried Leibniz en 1693.

Los "cuadrados mágicos" eran conocidos por los matemáticos árabes, posiblemente desde comienzos del siglo VII, quienes a su vez pudieron tomarlos de los matemáticos y astrónomos de la India, junto con otros aspectos de las matemáticas combinatorias. Todo esto sugiere que la idea provino de China. Los primeros "cuadrados mágicos" de orden 5 y 6 aparecieron en Bagdad en el 983, en la Enciclopedia de la Hermandad de Pureza (Rasa'il Ihkwan al-Safa).^[2]​

Después del desarrollo de la teoría de determinantes por Seki Kowa y Leibniz para facilitar la resolución de ecuaciones lineales, a finales del siglo XVII, Cramer presentó en 1750 la ahora denominada regla de Cramer. Carl Friedrich Gauss y Wilhelm Jordan desarrollaron la eliminación de Gauss-Jordan en el siglo XIX.

Fue James Joseph Sylvester quien utilizó por primera vez el término « matriz » en 1848/1850.

En 1853, Hamilton hizo algunos aportes a la teoría de matrices. Cayley introdujo en 1858 la notación matricial, como forma abreviada de escribir un sistema de m ecuaciones lineales con n incógnitas.

Cayley, Hamilton, Hermann Grassmann, Frobenius, Olga Taussky-Todd y John von Neumann cuentan entre los matemáticos famosos que trabajaron sobre la teoría de las matrices.
En 1925, Werner Heisenberg redescubre el cálculo matricial fundando una primera formulación de lo que iba a pasar a ser la mecánica cuántica. Se le considera a este respecto como uno de los padres de la mecánica cuántica.

Olga Taussky-Todd (1906-1995), durante la II Guerra Mundial, usó la teoría de matrices para investigar el fenómeno de aeroelasticidad llamado fluttering.

Introducción

Definición

Una matriz es un arreglo bidimensional de números (llamados entradas de la matriz) ordenados en filas (o renglones) y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. A una matriz con m filas y n columnas se le denomina matriz m-por-n (escrito m×n{displaystyle mtimes n}) donde m,n∈N−{0}{displaystyle m,nin mathbb {N} -{0}}. El conjunto de las matrices de tamaño m×n{displaystyle mtimes n} se representa como Mm×n(K){displaystyle {mathcal {M}}_{mtimes n}(mathbb {K} )}, donde K{displaystyle mathbb {K} } es el campo al cual pertenecen las entradas. El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después.

Dos matrices se dice que son iguales si tienen el mismo tamaño y los mismos elementos en las mismas posiciones.A la entrada de una matriz que se encuentra en la fila i−{displaystyle i-,!}ésima y la columna j−{displaystyle j-,!}ésima se le llama entrada i,j{displaystyle i,j,!} o entrada (i,j){displaystyle (i,j),!}-ésimo de la matriz. En estas expresiones también se consideran primero las filas y después las columnas.

Dos matrices A,B∈Mm×n(K){displaystyle A,Bin {mathcal {M}}_{mtimes n}(mathbb {K} )} son iguales si los elementos correspondientes son iguales, es decir, aij=bij,1≤i≤m,1≤j≤n{displaystyle a_{ij}=b_{ij},1leq ileq m,1leq jleq n}.

Para definir el concepto de matriz, el término "arreglo bidimensional" es útil, aunque poco formal, pero puede formalizarse usando el concepto de función. De este modo, una matriz de n filas y m columnas con entradas en un campo K{displaystyle mathbb {K} } es una función cuyo dominio es el conjunto de los pares ordenados (i,j){displaystyle (i,j),!}, donde 1≤i≤n{displaystyle 1leq ileq n} y 1≤j≤m{displaystyle 1leq jleq m}, y cuyo contradominio es K{displaystyle mathbb {K} }. Con esta definición, la entrada i,j{displaystyle i,j,!} es el valor de la función en el par ordenado (i,j){displaystyle (i,j),!}.

Se denota a las matrices con letra mayúscula, mientras que se utiliza la correspondiente letra en minúsculas para denotar a las entradas de las mismas, con subíndices que refieren al número de fila y columna del elemento.^[4]​Por ejemplo, al elemento de una matriz A{displaystyle A} de tamaño n×m{displaystyle ntimes m} que se encuentra en la fila i−{displaystyle i-,!}ésima y la columna j−{displaystyle j-,!}ésima se le denota como aij{displaystyle a_{ij},!}, donde 1≤i≤n{displaystyle 1leq ileq n} y 1≤j≤m{displaystyle 1leq jleq m}.

Cuando se va a representar explícitamente una entrada la cual está indexada con un i{displaystyle i,!} o un j{displaystyle j,!} con dos cifras se introduce una coma entre el índice de filas y de columnas. Así por ejemplo, la entrada que está en la primera fila y la segunda columna de la matriz A{displaystyle A,!} de tamaño 50×100{displaystyle 50times 100} se representa como a1,2{displaystyle a_{1,2},!} mientras que la entrada que está en la fila número 23 y la columna 100 se representa como a23,100{displaystyle a_{23,100},!}.

Además de utilizar letras mayúsculas para representar matrices, numerosos autores representan a las matrices con fuentes en negrita para distinguirlas de otros objetos matemáticos.^{[cita requerida]} Así A{displaystyle mathbf {A} } es una matriz, mientras que A{displaystyle A,!} es un escalar en esa notación. Sin embargo esta notación generalmente se deja para libros y publicaciones, donde es posible hacer esta distinción tipográfica con facilidad. En otras notaciones se considera que el contexto es lo suficientemente claro como para no usar negritas.

Otra notación, en sí un abuso de notación, representa a la matriz por sus entradas, i.e. A:=(aij){displaystyle A:=(a_{ij}),!} o incluso A:=aij{displaystyle A:=a_{ij},!}.

Como caso particular de matriz, se definen los vectores fila y los vectores columna. Un vector fila o vector renglón es cualquier matriz de tamaño 1×n{displaystyle 1times n} mientras que un vector columna es cualquier matriz de tamaño m×1{displaystyle mtimes 1}.

A las matrices que tienen el mismo número de filas que de columnas, m=n{displaystyle m=n,!}, se les llama matrices cuadradas y el conjunto se denota Mn(K){displaystyle {mathcal {M}}_{n}(mathbb {K} )}

Ejemplo

Dada la matriz A∈M4×3(R){displaystyle Ain {mathcal {M}}_{4times 3}(mathbb {R} )}

A=[123127492605]{displaystyle A={begin{bmatrix}1&2&3\1&2&7\4&9&2\6&0&5\end{bmatrix}}}

es una matriz de tamaño 4×3{displaystyle 4times 3}. La entrada a23{displaystyle a_{23},!} es 7.

La matriz R∈M1×9(R){displaystyle Rin {mathcal {M}}_{1times 9}(mathbb {R} )}

R=[123456789]{displaystyle R={begin{bmatrix}1&2&3&4&5&6&7&8&9end{bmatrix}}}

es una matriz de tamaño 1×9{displaystyle 1times 9}: un vector fila con 9 entradas.

Operaciones básicas entre matrices

Las operaciones que se pueden hacer con matrices provienen de sus aplicaciones, sobre todo de las aplicaciones en álgebra lineal. De ese modo las operaciones, o su forma muy particular de ser implementadas, no son únicas.

Suma o adición

Sean A,B∈Mn×m(K){displaystyle A,Bin {mathcal {M}}_{ntimes m}(mathbb {K} )}

[221321232204]+[014140211022]=[235461443226]{displaystyle {begin{bmatrix}2&2&1\3&2&1\2&3&2\2&0&4end{bmatrix}}quad +quad {begin{bmatrix}0&1&4\1&4&0\2&1&1\0&2&2end{bmatrix}}quad =quad {begin{bmatrix}2&3&5\4&6&1\4&4&3\2&2&6end{bmatrix}}}

. Se define la operación de suma o adición de matrices como una operación binaria +:Mn×m(K)×Mn×m(K)⟶Mn×m(K){displaystyle +:{mathcal {M}}_{ntimes m}(mathbb {K} )times {mathcal {M}}_{ntimes m}(mathbb {K} )longrightarrow {mathcal {M}}_{ntimes m}(mathbb {K} )} tal que (A,B)↦C=A+B{displaystyle (A,B)mapsto C=A+B} y donde cij=aij+bij{displaystyle c_{ij}=a_{ij}+b_{ij},!} en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el campo K{displaystyle mathbb {K} }. Por ejemplo, la entrada c12{displaystyle c_{12},!} es igual a la suma de los elementos a12{displaystyle a_{12},!} y b12{displaystyle b_{12},!} lo cual es a12+b12{displaystyle a_{12}+b_{12},!}.

Veamos un ejemplo más explícito. Sea A,B∈M3(R){displaystyle A,Bin {mathcal {M}}_{3}(mathbb {R} )}

[132100122]+[105750211]=[1+13+02+51+70+50+01+22+12+1]=[237850333]{displaystyle {begin{bmatrix}1&3&2\1&0&0\1&2&2end{bmatrix}}+{begin{bmatrix}1&0&5\7&5&0\2&1&1end{bmatrix}}={begin{bmatrix}1+1&3+0&2+5\1+7&0+5&0+0\1+2&2+1&2+1end{bmatrix}}={begin{bmatrix}2&3&7\8&5&0\3&3&3end{bmatrix}}}

No es necesario que las matrices sean cuadradas:

A la luz de estos ejemplos es inmediato ver que dos matrices se pueden sumar solamente si ambas tienen el mismo tamaño. La suma de matrices, en el caso de que las entradas estén en un campo, poseen las propiedades de asociatividad, conmutatividad, existencia de elemento neutro aditivo y existencia de inverso aditivo. Esto es así ya que estas son propiedades de los campos en los que están las entradas de la matriz.

Propiedades de la suma de matrices

Sean A,B,C∈Mn×m(K){displaystyle A,B,Cin {mathcal {M}}_{ntimes m}(mathbb {K} )}, donde K{displaystyle mathbb {K} } es un campo entonces se cumplen las siguientes propiedades para la operación binaria +{displaystyle +}

• Asociatividad

(A+B)+C=A+(B+C){displaystyle (A+B)+C=A+(B+C),!}

Demostración

Dada la definición de la operación binaria +{displaystyle +,!} se sigue el resultado ya que (aij+bij)+cij=aij+(bij+cij){displaystyle (a_{ij}+b_{ij})+c_{ij}=a_{ij}+(b_{ij}+c_{ij}),!} debido a que aij,bij,cij∈K{displaystyle a_{ij},b_{ij},c_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}.

• Conmutatividad

(A+B)=(B+A){displaystyle (A+B)=(B+A),!}

Demostración

Dada la definición de la operación binaria +{displaystyle +,!} se sigue el resultado ya que aij+bij=bij+aij{displaystyle a_{ij}+b_{ij}=b_{ij}+a_{ij},!} debido a que aij,bij∈K{displaystyle a_{ij},b_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}.

• Existencia del elemento neutro aditivo

Existe 0∈Mn×m(K){displaystyle 0in {mathcal {M}}_{ntimes m}(mathbb {K} )} tal que

A+0=0+A=A{displaystyle A+0=0+A=A,!}

Demostración

Tómese 0∈Mn×m(K){displaystyle 0in {mathcal {M}}_{ntimes m}(mathbb {K} )} tal que 0ij=0K∈K{displaystyle 0_{ij}=0_{mathbb {K} }in mathbb {K} } para cualquier i,j{displaystyle i,j,!} (dónde este último es el elemento neutro aditivo en el campo, el cual existe necesariamente). Entonces para cualquier A∈Mn×m(K){displaystyle Ain {mathcal {M}}_{ntimes m}(mathbb {K} )} se sigue que A+0=A{displaystyle A+0=A,!} ya que aij+0ij=aij+0K=aij{displaystyle a_{ij}+0_{ij}=a_{ij}+0_{mathbb {K} }=a_{ij}} para cualquier i,j{displaystyle i,j,!}, dado que las entradas están en un campo.

• Existencia del inverso aditivo

Existe D∈Mn×m(K){displaystyle Din {mathcal {M}}_{ntimes m}(mathbb {K} )} tal que

A+D=0{displaystyle A+D=0,!}

a esta matriz D{displaystyle D,!} se le denota por −A{displaystyle -A,!}.

Demostración

Dada A∈Mn×m(K){displaystyle Ain {mathcal {M}}_{ntimes m}(mathbb {K} )} tómese D∈Mn×m(K){displaystyle Din {mathcal {M}}_{ntimes m}(mathbb {K} )} tal que A+D=0{displaystyle A+D=0,!}. Entonces aij+dij=0ij=0K{displaystyle a_{ij}+d_{ij}=0_{ij}=0_{mathbb {K} }}; luego, por las propiedades de campo dij=−aij{displaystyle d_{ij}=-a_{ij},!} donde −aij{displaystyle -a_{ij},!} es el inverso aditivo de aij{displaystyle a_{ij},!} en el campo para cualquier i,j{displaystyle i,j,!}.

En efecto, estas propiedades dependen del conjunto en el que estén las entradas, como se ha dicho antes, aunque en las aplicaciones generalmente los campos usados son R{displaystyle mathbb {R} } (los números reales) y C{displaystyle mathbb {C} } (los números complejos).

Por como se definió la operación binaria adición se dice que ésta operación es una operación interna por lo que se cumple intrínsecamente la propiedad de que Mn×m(K){displaystyle {mathcal {M}}_{ntimes m}(mathbb {K} )} es cerrado bajo adición. Con éstas propiedades se tiene que (Mn×m(K),+){displaystyle ({mathcal {M}}_{ntimes m}(mathbb {K} ),+)} es un grupo abeliano.

En el caso en que el conjunto al que pertenecen las entradas de la matriz sea un anillo (A,+A,⋅A){displaystyle (A,+_{A},cdot _{A})}, la operación de adición de matrices continúa dotando de estructura de grupo abeliano a (Mn×m(A),+){displaystyle ({mathcal {M}}_{ntimes m}(A),+)}, ya que bajo un anillo (A,+A,⋅A){displaystyle (A,+_{A},cdot _{A})} se tiene que (A,+A){displaystyle (A,+_{A}),!} es un grupo abeliano. En el caso de que las entradas estén en un grupo (G,+G){displaystyle (G,+_{G}),!}, éste necesita ser un grupo abeliano para que la adición de matrices siga dotando de estructura de grupo abeliano a (Mn×m(G),+){displaystyle ({mathcal {M}}_{ntimes m}(G),+)}.

Producto por un escalar

Sean A∈Mn×m(K){displaystyle Ain {mathcal {M}}_{ntimes m}(mathbb {K} )} y λ∈K{displaystyle lambda in mathbb {K} }. Se define la operación de producto por un escalar como una función K×Mn×m(K)⟶Mn×m(K){displaystyle mathbb {K} times {mathcal {M}}_{ntimes m}(mathbb {K} )longrightarrow {mathcal {M}}_{ntimes m}(mathbb {K} )} tal que (λ,A)↦B=λA{displaystyle (lambda ,A)mapsto B=lambda A} y donde bij=λaij{displaystyle b_{ij}=lambda a_{ij},!} en donde el producto es la operación binaria correspondiente pero en el campo K{displaystyle mathbb {K} }. Por ejemplo, la entrada b12{displaystyle b_{12},!} es igual al producto λa12{displaystyle lambda a_{12},!}.

Veamos un ejemplo más explícito. Sea A∈M2×3(R){displaystyle Ain {mathcal {M}}_{2times 3}(mathbb {R} )} y 2∈R{displaystyle 2in mathbb {R} }

2[1 8−34−26]=[2(1)2(8)2(−3)2(4)2(−2)2(6)]=[216−68−412]{displaystyle 2{begin{bmatrix}1&,, ,8&-3\4&-2&,,,6end{bmatrix}}={begin{bmatrix}2(1)&,,,,2(8)&2(-3)\2(4)&2(-2)&,,,,2(6)end{bmatrix}}={begin{bmatrix}2&,16&-6\8&-4&,12end{bmatrix}}}

También es inmediato observar que el producto por un escalar da como resultado una matriz del mismo tamaño que la original. También el producto por un escalar dependerá de la estructura algebraica en la que las entradas están. En el caso de que estén en un campo serán dos distributividades (una respecto de suma de matrices y otra respecto de suma en el campo), asociatividad y una propiedad concerniente al producto por el elemento neutro multiplicativo del campo. A continuación se presentan las propiedades.

Propiedades del producto por un escalar

Sean A,B∈Mn×m(K){displaystyle A,Bin {mathcal {M}}_{ntimes m}(mathbb {K} )} y λ,μ∈K{displaystyle lambda ,mu in mathbb {K} }, donde K{displaystyle mathbb {K} } es un campo, entonces se cumplen las siguientes propiedades para la operación producto por un escalar

• Asociatividad

(λμ)A=λ(μA){displaystyle (lambda mu )A=lambda (mu A),!}

Demostración

Dada la definición de la operación se sigue el resultado ya que (λμ)aij=λ(μaij){displaystyle (lambda mu )a_{ij}=lambda (mu a_{ij}),!} debido a que aij∈K{displaystyle a_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}.

• Distributividad respecto de la suma de matrices

λ(A+B)=λA+λB{displaystyle lambda (A+B)=lambda A+lambda B,!}

Demostración

Dada la definición de la operación se sigue el resultado ya que λ(aij+bij)=λaij+λbij{displaystyle lambda (a_{ij}+b_{ij})=lambda a_{ij}+lambda b_{ij},!} debido a que aij,bij∈K{displaystyle a_{ij},b_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}.

• Distributividad respecto de la suma en el campo

(λ+μ)A=λA+μA{displaystyle (lambda +mu )A=lambda A+mu A,!}

Demostración

Dada la definición de la operación se sigue el resultado ya que (λ+μ)aij=λaij+μaij{displaystyle (lambda +mu )a_{ij}=lambda a_{ij}+mu a_{ij},!} debido a que aij∈K{displaystyle a_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}.

• Producto por el neutro multiplicativo del campo

1KA=A{displaystyle 1_{mathbb {K} }A=A,!}

Demostración

Dada la definición de la operación se sigue el resultado ya que 1K(aij)=aij{displaystyle 1_{mathbb {K} }(a_{ij})=a_{ij}} debido a que aij∈K{displaystyle a_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}.

Por como se definió la operación de producto por escalares se dice que Mn×m(K){displaystyle {mathcal {M}}_{ntimes m}(mathbb {K} )} es cerrado bajo producto por escalares. Con éstas propiedades y las de la adición se tiene que Mn×m(K){displaystyle {mathcal {M}}_{ntimes m}(mathbb {K} )} es un espacio vectorial con las operaciones de suma y producto por escalares definidas antes.

En el caso de que las entradas y los escalares no estén en un campo sino en un anillo entonces no necesariamente existe el neutro multiplicativo. En caso de que exista, con lo cual el anillo es un anillo con uno, se dice que Mn×m(A){displaystyle {mathcal {M}}_{ntimes m}(A)} es un módulo sobre A{displaystyle A,!}.

Ahora, a partir de las propiedades básicas se puede demostrar inmediatamente que

Demostración

Dada la definición de la operación se sigue el resultado ya que cij=λ(0ij)=λ(0K)=0K{displaystyle c_{ij}=lambda (0_{ij})=lambda (0_{mathbb {K} })=0_{mathbb {K} }} para todo i,j{displaystyle i,j,!}

Demostración

Dada la definición de la operación se sigue el resultado ya que cij=0K(aij)=0K{displaystyle c_{ij}=0_{mathbb {K} }(a_{ij})=0_{mathbb {K} }} para todo i,j{displaystyle i,j,!} debido a que aij∈K{displaystyle a_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}.

Demostración

Dada la definición de la operación se sigue el resultado ya que como en un campo no hay divisores de cero entonces λ(aij)=0K{displaystyle lambda (a_{ij})=0_{mathbb {K} }} para todo i,j{displaystyle i,j,!} implica que λ=0K{displaystyle lambda =0_{mathbb {K} }} o aij=0K{displaystyle a_{ij}=0_{mathbb {K} }}para todo i,j{displaystyle i,j,!}, i.e. A=0{displaystyle A=0,!}. No es posible un caso en el que sólo algunas entradas de la matriz sean cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo que hay divisores de cero y llegaríamos a una contradicción, ya que la suposición es que las entradas y los escalares están en un campo.

Demostración

Dada la definición de la operación se sigue el resultado ya que (−λ)(aij)=(−1K(λ))aij=(λ(−1K))aij=λ(−1K(aij))=λ(−aij){displaystyle (-lambda )(a_{ij})=(-1_{mathbb {K} }(lambda ))a_{ij}=(lambda (-1_{mathbb {K} }))a_{ij}=lambda (-1_{mathbb {K} }(a_{ij}))=lambda (-a_{ij})} debido a que aij∈K{displaystyle a_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}.

Este último resultado permite usar la notación −λA{displaystyle -lambda A,!} sin riesgo de ambigüedad.

Producto de matrices

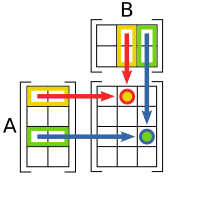
Diagrama esquemático que ilustra el producto de dos matrices A{displaystyle A,!} y B{displaystyle B,!} dando como resultado la matriz AB{displaystyle AB,!}.

El producto de matrices se define de una manera muy peculiar y hasta caprichosa cuando no se conoce su origen. El origen proviene del papel de las matrices como representaciones de aplicaciones lineales. Así el producto de matrices, como se define, proviene de la composición de aplicaciones lineales. En este contexto, el tamaño de la matriz corresponde con las dimensiones de los espacios vectoriales entre los cuales se establece la aplicación lineal. De ese modo el producto de matrices, representa la composición de aplicaciones lineales.

En efecto, en ciertas bases tenemos que f:V⟶W{displaystyle f:Vlongrightarrow W} se puede representar como f(x)=Ax{displaystyle f(x)=Ax,!} donde x{displaystyle x,!} es la representación de un vector de V{displaystyle V,!} en la base que se ha elegido para V{displaystyle V,!} en forma de vector columna. Si tenemos dos aplicaciones lineales f:V⟶W{displaystyle f:Vlongrightarrow W} y g:W⟶U{displaystyle g:Wlongrightarrow U} entonces f(x)=Bx{displaystyle f(x)=Bx,!} y g(x)=Ax{displaystyle g(x)=Ax,!}, luego la aplicación g∘f:V⟶U{displaystyle gcirc f:Vlongrightarrow U} se representará como g∘f(x)=g(f(x))=g(Bx)=ABx{displaystyle gcirc f(x)=g(f(x))=g(Bx)=ABx} donde AB{displaystyle AB,!} es el producto de las representaciones matriciales de f,g{displaystyle f,g,!}. Nótese que la composición no se puede dar entre cualquier aplicación sino entre aplicaciones que vayan de V→W→U{displaystyle Vrightarrow Wrightarrow U,!}, en particular debe de haber una relación entre las dimensiones de los espacios vectoriales. Una vez dicho esto podemos definir el producto de la siguiente manera.

Sean A∈Mn×m(K){displaystyle Ain {mathcal {M}}_{ntimes m}(mathbb {K} )} y B∈Mm×p(K){displaystyle Bin {mathcal {M}}_{mtimes p}(mathbb {K} )}. Se define el producto de matrices como una función Mn×m(K)×Mm×p(K)⟶Mn×p(K){displaystyle {mathcal {M}}_{ntimes m}(mathbb {K} )times {mathcal {M}}_{mtimes p}(mathbb {K} )longrightarrow {mathcal {M}}_{ntimes p}(mathbb {K} )} tal que (A,B)↦C=AB{displaystyle (A,B)mapsto C=AB} y donde cij=∑k=1maikbkj{displaystyle c_{ij}=sum _{k=1}^{m}a_{ik}b_{kj}} para toda i,j{displaystyle i,j,!}, es decir cij=ai1b1j+ai2b2j+ai3b3j+⋯+aimbmj{displaystyle c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+a_{i3}b_{3j}+dots +a_{im}b_{mj},!}. Por ejemplo, la entrada
c12=a11b12+a12b22+a13b32+⋯+a1mbm2{displaystyle c_{12}=a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32}+dots +a_{1m}b_{m2}}.

Veamos un ejemplo más explícito. Sean A∈M2×3(R){displaystyle Ain {mathcal {M}}_{2times 3}(mathbb {R} )} y B∈M3×2(R){displaystyle Bin {mathcal {M}}_{3times 2}(mathbb {R} )}

[ 102−131][312110]=[1(3)+0(2)+2(1)1(1)+0(1)+2(0)−1(3)+3(2)+1(1)−1(1)+3(1)+1(0)]=[5142]{displaystyle {begin{bmatrix},, ,1&0&2\-1&3&1end{bmatrix}}{begin{bmatrix}3&1\2&1\1&0end{bmatrix}}={begin{bmatrix},,,,1(3)+0(2)+2(1)&,,,,1(1)+0(1)+2(0)\-1(3)+3(2)+1(1)&-1(1)+3(1)+1(0)\end{bmatrix}}={begin{bmatrix}5&1\4&2\end{bmatrix}}}

dónde la matriz producto es como habíamos establecido en la definición: una matriz C∈M2×2(R){displaystyle Cin {mathcal {M}}_{2times 2}(mathbb {R} )}.

Sin tomar en cuenta la motivación que viene desde las aplicaciones lineales, es evidente ver que si ignoramos la definición de la función de producto de matrices y sólo se toma en cuenta la definición de las entradas, el producto no estará bien definido, ya que si A{displaystyle A,!} no tiene el mismo número de columnas que B{displaystyle B,!} de filas entonces no podremos establecer en donde acaba la suma: si la acabamos en el mayor de éstos números habrá sumandos que no están definidos ya que una de las matrices no tendrá más entradas, mientras que si tomamos el menor habrá entradas de alguna de las matrices que no se tomen en cuenta. Así es necesario que A{displaystyle A,!} tenga el mismo número de columnas que B{displaystyle B,!} de filas para que AB{displaystyle AB,!} exista.

Como se puede suponer también, las propiedades de ésta operación serán más limitadas en la generalidad ya que además de las limitaciones impuestas por la naturaleza de las entradas está esta limitación respecto a tamaño. Es claro, además, que el producto de matrices no siempre es una operación interna.

Propiedades del producto de matrices

Sean A,B,C{displaystyle A,B,C,!} matrices con entradas en K{displaystyle mathbb {K} }, donde K{displaystyle mathbb {K} } es un campo, entonces se cumplen las siguientes propiedades para el producto de matrices (considerando que los productos existan)

• Asociatividad

A(BC)=(AB)C{displaystyle A(BC)=(AB)C,!}

Demostración

Dada la definición de la operación se sigue el resultado ya que, si A(BC)=AH=R{displaystyle A(BC)=AH=R,!}, rij=∑k=1maikhkj{displaystyle r_{ij}=sum _{k=1}^{m}a_{ik}h_{kj},!} y hij=∑ℓ=1pbiℓcℓj{displaystyle h_{ij}=sum _{ell =1}^{p}b_{iell }c_{ell j},!} por lo que rij=∑k=1maik∑ℓ=1pbkℓcℓj=∑ℓ=1p∑k=1maikbkℓcℓj=∑ℓ=1psiℓcℓj=tij{displaystyle r_{ij}=sum _{k=1}^{m}a_{ik}sum _{ell =1}^{p}b_{kell }c_{ell j}=sum _{ell =1}^{p}sum _{k=1}^{m}a_{ik}b_{kell }c_{ell j}=sum _{ell =1}^{p}s_{iell }c_{ell j}=t_{ij},!} donde (AB)C=SC=T{displaystyle (AB)C=SC=T,!} debido a que aij,bij,cij∈K{displaystyle a_{ij},b_{ij},c_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}. Aquí estamos considerando que A{displaystyle A,!} es n×m{displaystyle ntimes m}, B{displaystyle B,!} es m×p{displaystyle mtimes p} y C{displaystyle C,!} es p×q{displaystyle ptimes q}.

• Distributividad respecto de la suma de matrices por la derecha

(A+B)C=AC+BC{displaystyle (A+B)C=AC+BC,!}

Demostración

Dada la definición de la operación se sigue el resultado ya que ∑k=1m(aik+bik)ckj=∑k=1maikckj+bikckj=∑k=1maikckj+∑k=1mbikckj{displaystyle sum _{k=1}^{m}(a_{ik}+b_{ik})c_{kj}=sum _{k=1}^{m}a_{ik}c_{kj}+b_{ik}c_{kj}=sum _{k=1}^{m}a_{ik}c_{kj}+sum _{k=1}^{m}b_{ik}c_{kj},!} debido a que aij,bij,cij∈K{displaystyle a_{ij},b_{ij},c_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}. Aquí estamos considerando que A{displaystyle A,!} es n×m{displaystyle ntimes m}, B{displaystyle B,!} es n×m{displaystyle ntimes m} y C{displaystyle C,!} es m×p{displaystyle mtimes p}.

• Distributividad respecto de la suma de matrices por la izquierda

A(B+C)=AB+AC{displaystyle A(B+C)=AB+AC,!}

Demostración

Dada la definición de la operación se sigue el resultado ya que ∑k=1maik(bkj+ckj)=∑k=1maikbkj+aikckj=∑k=1maikbkj+∑k=1maikckj{displaystyle sum _{k=1}^{m}a_{ik}(b_{kj}+c_{kj})=sum _{k=1}^{m}a_{ik}b_{kj}+a_{ik}c_{kj}=sum _{k=1}^{m}a_{ik}b_{kj}+sum _{k=1}^{m}a_{ik}c_{kj},!} debido a que aij,bij,cij∈K{displaystyle a_{ij},b_{ij},c_{ij}in mathbb {K} } para todo i,j{displaystyle i,j,!}. Aquí estamos considerando que A{displaystyle A,!} es n×m{displaystyle ntimes m}, B{displaystyle B,!} es m×p{displaystyle mtimes p} y C{displaystyle C,!} es m×p{displaystyle mtimes p}.

El producto de matrices no es conmutativo, si lo fuera la composición de funciones lineales sería conmutativa y eso en general no sucede. Obviamente existen casos particulares de algunos tipos de matrices en los que si hay conmutatividad. En el caso en que tengamos Mn(K){displaystyle {mathcal {M}}_{n}(mathbb {K} )} tendremos que el producto entre matrices en Mn(K){displaystyle {mathcal {M}}_{n}(mathbb {K} )} también está en Mn(K){displaystyle {mathcal {M}}_{n}(mathbb {K} )}. En ese caso Mn(K){displaystyle {mathcal {M}}_{n}(mathbb {K} )} además de espacio vectorial es un álgebra sobre un campo. En el caso de que el conjunto al que pertenecen las entradas sea un anillo conmutativo con uno entonces Mn(A){displaystyle {mathcal {M}}_{n}(A)} además de módulo es un álgebra sobre un anillo. Mas aún (Mn(K),+,⋅){displaystyle ({mathcal {M}}_{n}(mathbb {K} ),+,cdot )} con ⋅{displaystyle cdot } el producto de matrices es un anillo.

Otros conceptos relacionados con matrices

Rango de una matriz

El rango de una matriz A{displaystyle A,!} es la dimensión de la imagen de la aplicación lineal representada por A{displaystyle A,!}, que coincide con la dimensión de los espacios vectoriales generados por las filas o columnas de A{displaystyle A,!}.

Matriz traspuesta

La traspuesta de una matriz A∈Mn×m(X){displaystyle Ain {mathcal {M}}_{ntimes m}(X),!}, donde X{displaystyle X,!} no es necesariamente un campo, es una matriz B∈Mm×n(X){displaystyle Bin {mathcal {M}}_{mtimes n}(X),!} tal que bij=aji{displaystyle b_{ij}=a_{ji},!}. Por ejemplo la entrada b12=a21{displaystyle b_{12}=a_{21},!}.

Veamos un ejemplo más explícito. Sea A∈M2×3(R){displaystyle Ain {mathcal {M}}_{2times 3}(mathbb {R} )}

[1 8−34−2 6]{displaystyle {begin{bmatrix}1&,, ,8&-3\4&-2&,, 6end{bmatrix}}}

entonces su traspuesta es

[ 1 4 8−2−36]{displaystyle {begin{bmatrix},, ,1&,, ,4\,, ,8&-2\-3&,,,,6end{bmatrix}}}

Así, informalmente podríamos decir que la traspuesta es aquella matriz que se obtiene de la original cambiando filas por columnas. Las notaciones usuales para denotar la traspuesta de una matriz son AT,At{displaystyle A^{T},A^{t},!}.

La trasposición de matrices tiene las siguientes propiedades (donde ahora sí el conjunto de entradas debe ser al menos un anillo conmutativo):

(AT)T=A,(A+B)T=AT+BT,(AB)T=BTAT,{displaystyle {begin{aligned}&(A^{T})^{T}=A,\&(A+B)^{T}=A^{T}+B^{T},\&(AB)^{T}=B^{T}A^{T},\end{aligned}}}

Si A∈Mn×m(X){displaystyle Ain {mathcal {M}}_{ntimes m}(X),!} representa una aplicación lineal, entonces la matriz AT{displaystyle A^{T},!} describe la traspuesta de la aplicación lineal.

Matrices cuadradas y definiciones relacionadas

Una matriz cuadrada es una matriz que tiene el mismo número de filas que de columnas. El conjunto de todas las matrices cuadradas n-por-n junto a la suma y la multiplicación de matrices, es un anillo que generalmente no es conmutativo.

M(n,R), el anillo de las matrices cuadradas reales, es un álgebra asociativa real unitaria. M(n,C), el anillo de las matrices cuadradas complejas, es un álgebra asociativa compleja.

La matriz identidad I_n de orden n es la matriz n por n en la cual todos los elementos de la diagonal principal son iguales a 1 y todos los demás elementos son iguales a 0. La matriz identidad se denomina así porque satisface las ecuaciones MI_n = M y I_nN = N para cualquier matriz M m por n y N n por k.
Por ejemplo, si n = 3:

I3=[100010001].{displaystyle mathbf {I} _{3}={begin{bmatrix}1&0&0\0&1&0\0&0&1end{bmatrix}}.}

La matriz identidad es el elemento unitario en el anillo de matrices cuadradas.

Los elementos invertibles de este anillo se llaman matrices invertibles, regulares o no singulares. Una matriz A n por n es invertible si y sólo si existe una matriz B tal que AB = I

(left)

En este caso, B es la matriz inversa de A, identificada por A^-1 .
El conjunto de todas las matrices invertibles n por n forma un grupo (concretamente un grupo de Lie) bajo la multiplicación de matrices, el grupo lineal general.

Si λ es un número y v es un vector no nulo tal que Av = λv, entonces se dice que v es un vector propio de A y que λ es su valor propio asociado. El número λ es un valor propio de A si y sólo si A−λI_n no es invertible, lo que sucede si y sólo si p_A(λ) = 0, donde p_A(x) es el polinomio característico de A. p_A(x) es un polinomio de grado n y por lo tanto, tiene n raíces complejas múltiples raíces si se cuentan de acuerdo a su multiplicidad. Cada matriz cuadrada tiene como mucho n valores propios complejos.

El determinante de una matriz cuadrada A es el producto de sus n valores propios, pero también puede ser definida por la fórmula de Leibniz. Las matrices invertibles son precisamente las matrices cuyo determinante es distinto de cero.

El algoritmo de eliminación gaussiana puede ser usado para calcular el determinante, el rango y la inversa de una matriz y para resolver sistemas de ecuaciones lineales.

La traza de una matriz cuadrada es la suma de los elementos de la diagonal, lo que equivale a la suma de sus n valores propios.

Una matriz de Vandermonde es una matriz cuadrada cuyas filas son las potencias de un número. Su determinante es fácil de calcular.

Matriz Lógica

Una matriz lógica, matriz binaria, matriz de relación, matriz booleana o matriz (0,1) es una matriz con entradas del dominio booleano B={0,1}{displaystyle B={0,1}}. Tal matriz puede ser usada para representar una relación binaria entre un par de conjuntos finitos.

Representación de una relación matricial

Si R{displaystyle R} es una relación binaria entre los finitos conjuntos ordenados X{displaystyle X} e Y{displaystyle Y} (tales que R⊆X⋅Y{displaystyle Rsubseteq Xcdot Y}), entonces R{displaystyle R} puede representarse por la matriz lógica M{displaystyle M} cuyos índices de fila y columna ordenan los elementos de X{displaystyle X} e Y{displaystyle Y}, respectivamente, tales que las entradas de M{displaystyle M} se definen por:

Mi,j={1(xi,yj)∈R0(xi,yj)∉R{displaystyle M_{i,j}={begin{cases}1&(x_{i},y_{j})in R\0&(x_{i},y_{j})not in Rend{cases}}}

Con el fin de designar los números de cada fila y columna de la matriz, los conjuntos X e Y están ordenados con números enteros positivos: i va desde 1 hasta la cardinalidad (tamaño) de X y j oscila entre 1 y la cardinalidad de Y.

Ejemplo

La relación binaria R en el conjunto {1, 2, 3, 4} se define de manera que aRb se lleva a cabo si y sólo si a divide b uniformemente, sin resto. Por ejemplo, 2R4 satisface la relación porque 2 divide 4 sin dejar un resto, pero 3R4 no porque cuando 3 divide 4 hay un resto de 1. El conjunto siguiente es el conjunto de pares para los que se mantiene la relación R.

{(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)}.

La representación correspondiente como matriz booleana es:

(1111010100100001).{displaystyle {begin{pmatrix}1&1&1&1\0&1&0&1\0&0&1&0\0&0&0&1end{pmatrix}}.}

Algunas Propiedades

La representación matricial de la relación de igualdad en un conjunto finito es la matriz de identidad, es decir, una matriz cuya diagonal principal es todo unos (1), mientras que el resto de elementos son ceros(0).
Si el dominio booleano es visto como un semianillo, donde la suma corresponde al OR lógico y la multiplicación al AND lógico, la representación matricial de la composición de dos relaciones es igual al producto de la matriz de las representaciones matriciales de esta relación. Este producto se puede calcular en el tiempo esperado O(n²).

Frecuentemente, las operaciones en matrices binarias están definidas en términos de la aritmética modular mod 2, es decir, los elementos se tratan como elementos del campo de Galois GF(2) = ℤ₂. Surgen una variedad de representaciones y tienen un número de formas especiales más restringidas. Se aplican por ejemplo en XOR-satisfacible (Inglés).

El número de matrices binarias mxn distintas es igual a 2^mn, y es, por consiguiente, finito.

Aplicaciones

Las matrices en la Computación

Las matrices son utilizadas ampliamente en la computación, por su facilidad y liviandad para manipular información. En este contexto, son una buena forma para representar grafos, y son muy utilizadas en el cálculo numérico.
En la computación gráfica, las matrices son ampliamente usadas para lograr animaciones de objetos y formas.

Ejemplo de brazo robótico

El mundo de las matrices es muy amplio aunque parezca tan simple, programas como Matlab pueden crear sistemas de matrices tan complejos que incluso al programa le es difícil resolverlos.
Aunque no lo parezca las matrices también se pueden aplicar al mundo de la computación y programación.

Un ejemplo sencillo sería el campo aplicado a la programación en lo que viene relacionado con la robótica ya que se utiliza en este caso el programa matlab para poder programar robots como puede ser un brazo biónico.
Un ejemplo sería el Lynx6.

El Lynx6 se considera un manipulador de 5 ejes de rotación (base, hombro, codo, movimiento y rotación de la muñeca); este brazo mecánico entrega movimientos rápidos, exactos y repetitivos, gracias a los servomotores que lleva incorporados. Como paso previo se debe desarrollar una aplicación que obtiene el modelo directo FK e inverso IK del brazo robótico.

Brazo Robótico

-El modelo FK consiste en encontrar una matriz de transformación homogénea T que relacione la posición cartesiana (Px, Py, PZ) y los ángulos de Euler (φ,ψ,θ) Escogiendo adecuadamente el sistema de coordenadas ligado a cada segmento es posible ir de un sistema referencial al siguiente por medio de 4 transformaciones básicas.

-Matriz de transformación (1) Donde es la matriz resultante que relaciona el sistema de referencia del segmento i-1 con el sistema de referencia del segmento ièsimo, Rotz(ϴ1) es la rotación alrededor del eje Z i-1 con un valor de ϴ1, T (0,0, di) es una traslación de una distancia di, a lo largo del eje Zi-1 , T (a1, 0,0) es una traslación de una distancia a1, a lo largo del eje Xi . Y finalmente Rotx(αi) es la rotación alrededor del eje de Xi, con un valor de αi

Los resultados van a depender exclusivamente de las características geométricas del brazo manipulador. En nuestro caso los parámetros físicos dependen de los valores de las articulaciones y longitud conocidos en cada sistema de coordenadas, deben expresarse y asignarse en términos de la convención D-H. Multiplicando las matrices individuales de la ecuación (1) en el orden correcto, la matriz de transformación, que resuelve los valores de posición y orientación en cada sistema de coordenadas es la ecuación (2 ) Los términos individuales de las tres primeras columnas de la matriz (n, o, a) representan la orientación del eje principal en el sistema de coordenadas. La última columna P indica la posición (x, y, z) del origen. Cada uno de los términos de la matriz pueden calcularse a partir de las ecuaciones siguientes :

La relación entre las matrices de transformación, forma la cadena cinemática de las articulaciones y segmentos consecutivos del brazo robótico. Donde T es la matriz de transformación homogénea buscada . Sustituyendo los parámetros de la tabla 2 en las matrices de transformación se obtienen estas ecuaciones.
Calculando la multiplicación no conmutativa de la ecuación (17, se obtiene la matriz de transformación homogénea: Donde (n, o, a) es una terna ortogonal que representa la orientación y P es un vector (Px, Py, Pz) que representa la posición del efector extremo del brazo. La solución obtenida para una posición en reposo del brazo con Θ1= 0º , θ2= 90º , θ3 =0º , θ4= -90º y θ5=0º

Teoría de matrices

La teoría de matrices es una rama de las matemáticas que se centra en el estudio de matrices. Inicialmente una rama secundaria del álgebra lineal, ha venido cubriendo también los temas relacionados con la teoría de grafos, el álgebra, la combinatoria y la estadística.

Matrices relacionadas con otros temas

Una matriz puede identificarse a una aplicación lineal entre dos espacios vectoriales de dimensión finita. Así la teoría de las matrices habitualmente se considera como una rama del álgebra lineal. Las matrices cuadradas desempeñan un papel particular, porque el conjunto de matrices de orden n (n entero natural no nulo dado) posee propiedades de « estabilidad » de operaciones.

Los conceptos de matriz estocástica y matriz doblemente estocástica son herramientas importantes para estudiar los procesos estocásticos, en probabilidad y en estadística.

Las matrices definidas positivas aparecen en la búsqueda de máximos y mínimos de funciones a valores reales, y a varias variables.

Es también importante disponer de una teoría de matrices a coeficientes en un anillo. En particular, las matrices a coeficientes en el anillo de polinomios se utilizan en teoría de mandos.

En matemáticas puras, los anillos de matrices pueden proporcionar un rico campo de contraejemplos para conjeturas matemáticas.

Matrices en teoría de grafos

En teoría de los grafos, a todo grafo etiquetado corresponde la matriz de adyacencia. Una matriz de permutación es una matriz que representa una permutación; matriz cuadrada cuyos coeficientes son 0 o 1, con un solo 1 en cada línea y cada columna. Estas matrices se utilizan en combinatorio.

También existe otro tipo de matriz además de la matriz de adyacencia que es la conocida como matriz de incidencia en la cual el grafo se muestra en una matriz de A (serían las aristas) por V (serían los vértices), donde contiene la información de la arista (1 si está conectado y 0 no conectado).

Si nos dan un grafo G=(X,U){displaystyle G=(X,U)}, de orden n{displaystyle n}, podemos llegar a representar una relación de adyacencia, mediante una matriz A=[aij]{displaystyle A=[a_{ij}]} nxn, también llamada matriz de adyacencia de G.

Se deben de tener en cuenta una serie de observaciones sobre esto:

1. La matriz de adyacencia es una matriz booleana, como se ha dicho antes es una matriz que solo puede contener 0 y 1.


2. Σ_i x_ij = semigrado exterior de x_i
   


3. Σ_j x_ij = semigrado interior de x_j
   

En la teoría de grafos, se llama matriz de un grafo a la matriz que indica en la línea i y la columna j el número de aristas que enlazan el vértice i al vértice j. En un grafo no orientado, la matriz es simétrica. La suma de los elementos de una columna permite determinar el grado de un vértice. La matriz Mn{displaystyle M^{n}} indica en la línea i y la columna j el número de caminos a n aristas que adjuntan el vértice i al vértice j.

Grafo sobre el que se realiza el estudio.

A continuación mostraremos un ejemplo de un grafo y su matriz de adyacencia:

La matriz de adyacencia de este grafo vendría dada de la forma:

La matriz de adyacencia se basa en las conexiones que se realizan entre los vértices del grafo apareciendo así un 1 en los casos en los que dos vértices están conectados y un 0 en los casos en los que no.

En algunos casos como el de la posición V₃/V₅ se observa un 0 debido a que la conexión entre ellos muestra un sentido permitiendo el paso de flujo de V₅ a V₃ pero no al contrario, motivo por el cual V₅/V₃ si presenta un 1.

Cabe decir que si se toma otra ordenación de los vértices la matriz de adyacencia sera diferente, pero todas las matrices de adyacencia resultantes de un mismo grafo están unidas por una matriz de permutación P tal que P^-1 C P = A (Siendo C y A dos matrices de adyacencia distintas pero provenientes de un mismo grafo).

Análisis y geometría

La Matriz de Hessian de una función diferencial ƒ: Rⁿ → R consiste en la segunda derivada de f con respecto a las varias direcciones de coordenadas, esto es,

H(f)=[∂2f∂xi∂xj].{displaystyle H(f)=left[{frac {partial ^{2}f}{partial x_{i},partial x_{j}}}right].}

En el punto de silla de montar (x = 0, y = 0) (rojo) de la función f(x,−y) = x² − y², la Matriz de Hessians [200−2]{displaystyle {begin{bmatrix}2&0\0&-2end{bmatrix}}} es indefinida.

Codifica información sobre el comportamiento creciente de la función: dando un punto crítico x = (x₁, ..., x_n), esto es, un punto donde la primera derivada parcial ∂f/∂xi{displaystyle partial f/partial x_{i}} de ƒ desaparece, la función tiene un mínimo local si la matriz de Hessian es definida positiva para todos sus valores. La programación cuadrática puede usarse para encontrar mínimos y máximos globales de una función cuadrática estrechamente relacionadas con las asociadas a matrices.

Otra matriz frecuentemente utilizada en situaciones geométricas el la Matriz Jacobi de un mapa diferenciable f: Rⁿ → R^m. Si f₁, ..., f_m indica los componentes de f, entonces la matriz Jacobi es definada como

J(f)=[∂fi∂xj]1≤i≤m,1≤j≤n.{displaystyle J(f)=left[{frac {partial f_{i}}{partial x_{j}}}right]_{1leq ileq m,1leq jleq n}.}

Si n > m, y si el rango de la matriz Jacobi alcanza su valor máximo m, f es localmente invertible en ese punto, por el teorema de la función implícita.
Las ecuaciones diferenciales parciales pueden clasificarse considerando la matriz de coeficientes de los operadores diferenciales de orden más alto de la ecuación. Para las ecuaciones diferenciales elípticas parciales esta matriz es positiva para todos sus valores, los cuales tienen una influencia decisiva en el grupo de soluciones posibles de la ecuación en cuestión.

El método de elementos finitos es un importante método numérico para resolver ecuaciones diferenciales parciales, extensamente aplicado en simulaciones de sistemas físicos complejos. Intenta aproximar la solución a alguna ecuación de funciones lineales pieza a pieza, donde las piezas son elegidas con respecto a una rejilla suficientemente fina, que a su vez puede ser refundida como una ecuación matricial.

Algunos teoremas

• Teorema de Cayley-Hamilton


• Teorema de Gerschgorin

Véase también

• Descomposición de Schur


• Descomposición en valores singulares


• Descomposición QR


• Determinante (matemática)


• Eliminación de Gauss-Jordan


• Factorización LU


• Forma canónica de Jordan


• Lema de Schur


• Matlab


• Matriz triangular

Referencias

• 
  Beezer, Rob, Un primer curso en álgebra lineal, licencia bajo GFDL. (En inglés)


• 
  Jim Hefferon: Álgebra lineal (Libros de texto en línea) (En inglés)

Notas

Enlaces externos

• 
  Una breve historia del álgebra lineal y de la teoría de matrices lineal (en inglés)
  


• 
  Matemáticas/Matrices(En Wikilibros)


• Reducir matrices por Gauss Jordan de manera Online


• Esta obra contiene una traducción parcial derivada de Matrix (mathematics) de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.


• Esta obra contiene una traducción parcial derivada de Logical Matrix de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.