Csdrhrt

Un óvalo con un eje de simetría

El término óvalo (del latín ovum, huevo) hace referencia a una forma geométrica convexa y redondeada, que se asemeja al perfil de un huevo de ave en su sentido más amplio.

Incluye a circunferencias y elipses como casos especiales, con dos ejes de simetría en lugar de solamente uno o ninguno.

El uso del término no siempre es consistente, en ocasiones también se usa de manera puramente descriptiva. Sin embargo, en el análisis matemático se puede definir formalmente como un tipo de curvas planas. En este contexto, también se habla de curvas o líneas ovaladas.

Un cuerpo convexo redondeado y tridimensional (generalmente un subconjunto convexo cerrado de Rn{displaystyle mathbb {R} ^{n}}) se conoce como ovoide.^[1]​ En este sentido, un óvalo con los puntos de su interior es entonces un ovoide de dos dimensiones.

En geometría proyectiva los términos curva ovalada y ovoide (sin atender a su diferenciabilidad) según sus condiciones de convexidad, se establecen utilizando exclusivamente condiciones de incidencia ("cada recta corta a un óvalo u ovoide en a lo sumo dos puntos"), en lo que se define como un conjunto cuadrático. En sentido proyectivo, un óvalo en el plano real requiere además la condición de que ningún punto de su contorno tenga curvatura nula. Tal óvalo es entonces el borde de un conjunto estrictamente convexo, por que no contiene segmentos rectilíneos.

Definición formal y propiedades

Óvalo sin ejes de simetría

La forma redondeada de un óvalo es la consecuencia de que una curva cerrada reúna las condiciones de suavidad y convexidad, de acuerdo con la siguiente definición:

Sin embargo, esta definición no abarca todas las figuras geométricas que a veces son denominadas óvalos. Por ejemplo, los óvalos compuestos por diferentes arcos circulares no cumplen esta definición, porque su segunda derivada no es continua en toda la curva. Si se desea contemplar también estos casos, entonces debe prescindirse de la condición de la suavidad de la curvatura (diferenciabilidad C0{displaystyle C^{0}} o C1{displaystyle C^{1}} en lugar de C2{displaystyle C^{2}}). En consecuencia, en algunos textos la definición de óvalo solo exige la condición de convexidad.^[5]​^[6]​ Sin embargo, esto tiene la desventaja de que la definición incluye entonces figuras que apenas son percibidos con forma de huevo, tales como los polígonos convexos.

Tal como se ha definido en el recuadro anterior, un óvalo tiene las siguientes propiedades:

Óvalo con rectas tangente, secante y pasante

• Un óvalo es una curva de Jordan, es decir, no tiene bucles ni lazos.


• La orientación de la curvatura de un óvalo no tiene cambios de signo, es decir, dependiendo del sentido de recorrido, esto significa que la curvatura orientada para cada punto del óvalo es siempre negativa o siempre positiva. De manera ilustrativa, esto significa que no presenta retrocesos ni hendiduras. Solo puede recorrerse mediante un giro completo de 360° a la izquierda o a la derecha.


• El interior de un óvalo es un conjunto convexo, y el óvalo forma su borde.


• En un óvalo es aplicable el teorema de los cuatro vértices, es decir, su ley de curvatura presenta al menos cuatro puntos extremos.^[7]​


• Si un punto del óvalo tiene una tangente, todo el óvalo está al mismo lado de la tangente.


• Si además se exige que la curvatura del óvalo no desaparezca en ninguna sección, es decir, que la curvatura adquiera el valor cero como máximo en puntos aislados, entonces la tangente anterior existe en cada punto del óvalo. Más en general: entonces, cualquier línea recta tiene en común con el óvalo exactamente dos puntos (secante), un punto (tangente) o ningún punto (pasante).

Ejemplos y construcciones

Los óvalos se pueden construir usando métodos completamente diferentes. Se obtienen varios procedimientos de construcción a partir de diversas técnicas de diseño de la elipse conveniente modificadas.

Es sabido que se puede generar una elipse cortando un cono con un un plano (véase sección cónica). Si en vez de un cono se utiliza otro cuerpo de revolución como un hiperboloide, de la intersección con un plano se obtienen diferentes óvalos. Una posibilidad adicional consiste en sustituir en la ecuación paramétrica (o en la ecuación algebraica) de una elipse, los parámetros constantes a y b (las longitudes de los semiejes) (a⋅cos⁡(t),b⋅sin⁡(t)){displaystyle (acdot cos(t),bcdot sin(t))} por las funciones x2a2+y2b2=1{displaystyle {tfrac {x^{2}}{a^{2}}}+{tfrac {y^{2}}{b^{2}}}=1}.

También se puede definir una elipse como el conjunto de puntos P, para los que la suma de las distancias a los dos focos F₁ y F₂ es (|F1P|+|F2P|=2a){displaystyle left(|F_{1}P|+|F_{2}P|=2aright)} constante. Si se reemplaza esta suma de las distancias por una suma ponderada (k1⋅|F1P|+k2⋅|F2P|=2a){displaystyle left(k_{1}cdot |F_{1}P|+k_{2}cdot |F_{2}P|=2aright)}, el conjunto de puntos forma un óvalo, que solo tiene un eje de simetría, en el que se sitúan un extremo romo y el otro puntiagudo. Tal óvalo coincide con la curva interior de un óvalo cartesiano.

El método de construcción de de La Hire crea una elipse usando dos circunferencias concéntricas. Si se desplaza un poco el centro del círculo exterior y se conservan los pasos restantes del proceso de construcción, se obtiene un (nuevo) óvalo, que posee un eje de simetría cuando se mueve el centro del círculo exterior en los ejes de la elipse. Si se mueve el centro fuera de los ejes, se crea un óvalo sin ejes de simetría.

• 
  

  

  
  

  
  

  Construcción con círcunferencias concéntricas
  

  
  

  
  


• 
  

  

  
  

  
  

  Construcción con círcunferencias excéntricas
  

  
  

  
  


• 
  

  

  
  

  
  

  Elipse: |F1P|+|F2P|=22,84{displaystyle |F_{1}P|+|F_{2}P|=22{,}84,}
  

  
  

  
  


• 
  

  

  
  

  
  

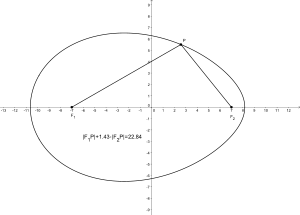
  |F1P|+1.43⋅|F2P|=22,84{displaystyle |F_{1}P|+{textbf {1.43}}cdot |F_{2}P|=22{,}84}
  

  
  

  
  


• 
  

  

  
  

  
  

  Elipse: x24+y21=1{displaystyle {frac {x^{2}}{4}}+{frac {y^{2}}{1}}=1}
  

  
  

  
  


• 
  

  

  
  

  
  

  x24+y21−0,2⋅x=1{displaystyle {frac {x^{2}}{4}}+{frac {y^{2}}{1-0{,}2cdot x}}=1}
  

  
  

  
  

El conjunto de soluciones de una ecuación con dos incógnitas o ciertos de sus subconjuntos a menudo se pueden considerar como curvas en el plano. Una ecuación adecuada produce un óvalo. Si tal curva solución del sistema no es ovalada, pero tiene un bucle convexo, se puede crear un óvalo agregando un término de corrección al bucle.

• 
  

  

  
  

  
  

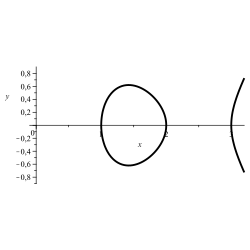
  Curva elíptica: y2=(x−1)⋅(x−2)⋅(x−3){displaystyle y^{2}=(x-1)cdot (x-2)cdot (x-3)}
  

  
  

  
  


• 
  

  

  
  

  
  

  Superelipse: (x2)4+(y1)4=1{displaystyle left({frac {x}{2}}right)^{4}+left({frac {y}{1}}right)^{4}=1}
  

  
  

  
  


• 
  

  

  
  

  
  

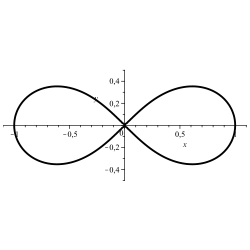
  Lemniscata: (x2+y2)2−(x2−y2)=0{displaystyle (x^{2}+y^{2})^{2}-(x^{2}-y^{2})=0,}
  

  
  

  
  


• 
  

  

  
  

  
  

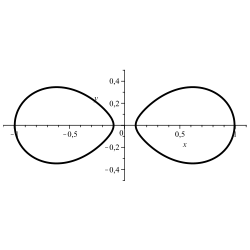
  Óvalo de Cassini: (x2+y2)2−(x2−y2)+0,01=0{displaystyle (x^{2}+y^{2})^{2}-(x^{2}-y^{2})+{textbf {0,01}}=0}
  

  
  

  
  


• 
  

  

  
  

  
  

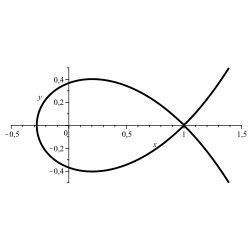
  Curva de Szegö: x2+y2=e2⋅x−2{displaystyle x^{2}+y^{2}=e^{2cdot x-2}}
  

  
  

  
  


• 
  

  

  
  

  
  

  x2+y2+0,02=e2⋅x−2{displaystyle x^{2}+y^{2}+{textbf {0,02}}=e^{2cdot x-2}}
  

  
  

  
  


• 
  

  

  
  

  
  

  Folium de Descartes: x3+y3=3⋅x⋅y{displaystyle x^{3}+y^{3}=3cdot xcdot y}
  

  
  

  
  


• 
  

  

  
  

  
  

  x3+y3+0,06=3⋅x⋅y{displaystyle x^{3}+y^{3}+{textbf {0,06}}=3cdot xcdot y}
  

  
  

  
  

Los óvalos también pueden estar compuestos por arcos y segmentos. Sin embargo, dichos óvalos tienen menos suavidad que la requerida en la definición anterior, porque solo verifican C1{displaystyle C^{1}} pero no C2{displaystyle C^{2}}. Aunque todavía son suaves en el sentido de una derivada constante, ya no tienen una curvatura continua. La curvatura es constante en las secciones, pero presenta un punto de discontinuidad en las uniones de los arcos circulares o de las secciones rectas.

Óvalos compuestos de arcos circulares y secciones rectas

Ejemplos de formas ovaladas comunes

Huevos de ave

Huevos de Pascua

Roscón de Reyes

Pista de atletismo

Balón de rugby

Véase también

• Óvalo de Cassini


• Curva elíptica


• Superelipse

Referencias

Bibliografía

• 
  A.B. Ivanov. «Oval». 
  


• 
  Helmut Reckziegel, Markus Kriener, Knut Pawel (1998). Elementare Differentialgeometrie mit Maple. Vieweg+Teubner Verlag. pp. 43 de 194. ISBN 9783528069919. Consultado el 28 de agosto de 2018. 
  


• 
  Helmut Reckziegel, Markus Kriener, Knut Pawel (1998). Elementare Differentialgeometrie mit Maple. Vieweg+Teubner Verlag. pp. 43 de 194. ISBN 9783528069919. Consultado el 28 de agosto de 2018. 
  


• John A. Adam: A Mathematical Nature Walk. Princeton University Press 2009, ISBN 978-0-691-12895-5, S. 124–136


• Arnold Emch: Some Properties of Closed Convex Curves in a Plane. American Journal of Mathematics, Band 35, Nr. 4 (Okt., 1913), S. 407–41 JSTOR 2370404
  

• N. Hansen Ball: On Ovals. The American Mathematical Monthly, Band 37, Nr. 7 (Aug. - Sep., 1930), S. 348–353 JSTOR 2299271
  

• 
  Charles Hutton (1815). A Philosophical and Mathematical Dictionary. Volumen 2. author. p. 141. Consultado el 28 de agosto de 2018. 
  

Enlaces externos

• 
  Wikimedia Commons alberga una categoría multimedia sobre Óvalos.


• 
  Weisstein, Eric W. «Oval». En Weisstein, Eric W. MathWorld (en inglés). Wolfram Research. 
  


• Norbert Harthun, Iris Rennert: Die Ei-Kurve als Schnitt des Hyperbolischen Kegels (PDF; 158 kB)


• 
  Egg curves auf mathematische-basteleien.de (englisch)


• Paul L. Rosin: On the Construction of Ovals (englisch; PDF; 405 kB)


• André Heck: Mathematical Brooding over an Egg. In Loci, August 2008 - Online-Journal der MAA
  


• 
  Egg Math - Sammlung von webbasierten Unterrichtseinheiten zur Mathematik rundum das Ei (en inglés)
  


• 
  Bibliografía relacionada con Óvalo en el catálogo de la Biblioteca Nacional de Alemania.