Elemento de un conjunto
En teoría de conjuntos, un elemento o miembro de un conjunto (o familia de conjuntos) es un objeto que forma parte de ese conjunto (o familia).
Índice
1 Teoría de conjuntos y elementos
2 Relación de pertenencia
3 Cardinalidad de conjuntos
4 Ejemplos
5 Referencias
6 Bibliografía
Teoría de conjuntos y elementos
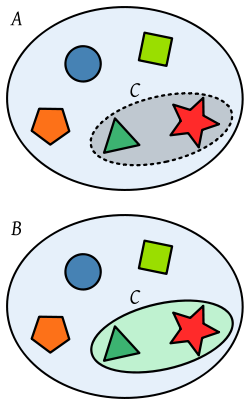
Diferencia entre elemento y subconjunto. El conjunto C está formado por dos elementos. El conjunto A está formado por cinco elementos (cinco figuras geométricas), y C, señalado con línea discontinua, es un subconjunto de A, C ⊆ A. El conjunto B, por el contrario, está formado por cuatro elementos: tres figuras geométricas y un conjunto, a saber, C. Por tanto, C, señalado con línea continua, es un elemento de B, C ∈ B.
Al escribir A={1,2,3,4}{displaystyle A={1,2,3,4}}




Los elementos pueden ser conjuntos en sí mismos. Por ejemplo, consideremos el conjunto B={1,2,{3,4}}{displaystyle B={1,2,{3,4}}}



Los elementos de un conjunto pueden ser cualquier cosa. Por ejemplo, C={rojo, verde, azul}{displaystyle C={{mbox{rojo, verde, azul}}}}
Relación de pertenencia
La relación «es un elemento de», también llamada miembro del conjunto, se denota mediante el símbolo ∈{displaystyle in }
- x∈A{displaystyle xin A}
estamos diciendo que x{displaystyle x}














No obstante lo anterior, los términos «A{displaystyle A}





Sean x{displaystyle x}

| Relación | Notación | Se lee |
|---|---|---|
| pertenencia | x∈A{displaystyle xin A} | x pertenece a A |
| inclusión | A⊂B{displaystyle Asubset B} | A está contenido en B |
A⊆B{displaystyle Asubseteq B} | A está contenido en B o es igual que B | |
| inclusión | A⊃B{displaystyle Asupset B} | A contiene a B |
A⊇B{displaystyle Asupseteq B} | A contiene a B o es igual que B |
Una barra cruzada sobre el símbolo niega el enunciado; por ejemplo x∉A{displaystyle xnot in A}
Cardinalidad de conjuntos
El número de elementos en un conjunto particular es una propiedad conocida como cardinalidad, que informalmente se conoce como el tamaño de un conjunto. Para los ejemplos anteriores, la cardinalidad del conjunto A{displaystyle A}



Ejemplos
Usando los conjuntos definidos arriba:
- B={1,2,{3,4}}{displaystyle B={1,2,{3,4}},}
podemos decir que:
- 2 ∈ B
- {3,4} ∈ B
∅ ⊂ B- { } ⊂ B
- {2} ⊂ B
- {1,2} ⊂ B
amarillo ∉ B- 8 ∉ B
card(B) = 3
card({3,4}) = 2- La cardinalidad de D = { 2, 4, 6, 8, 10, 12 } es finita e igual a 6.
- La cardinalidad de P = { 2, 3, 5, 7, 11, 13... } (los números primos) es infinita.
No podemos decir respecto al conjunto B, que:
- 2 ⊂ B (cuando usamos la inclusión, debemos relacionar subconjuntos y no elementos, por lo tanto deben de tener llaves a excepción del conjunto vacío (∅) )
- 3 ∈ {3,4} (porque la relación debe ser respecto al conjunto B y no a sus elementos)
- B ∈ B (porque B ⊂ B, no es un elemento de sí mismo)
Referencias
↑ Eric Schechter (1997). Handbook of Analysis and Its Foundations. Academic Press. ISBN 0-12-622760-8. p. 12
↑ 24.243 Classical Set Theory (lecture). Instituto Tecnológico de Massachusetts, Cambridge, MA. 4 de febrero de 1992.
Bibliografía
Paul R. Halmos 1960, Naive Set Theory, Springer-Verlag, NY, ISBN 0-387-90092-6.- Patrick Suppes 1960, 1972, Axiomatic Set Theory, Dover Publications, Inc. NY, ISBN 0-486-61630-4.

