Csdrhrt

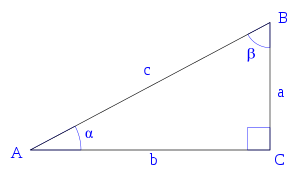
Triángulo rectángulo con sus tres lados y ángulos nombrados. El triángulo rectángulo cuyas longitudes de sus tres lados sean números enteros positivos, éstos forman una terna pitagórica, y evidentemente a2+b2=c2{displaystyle a^{2}+b^{2}=c^{2}}

Una terna pitagórica es un conjunto ordenado de tres números enteros positivos a, b, c, y son solución de la ecuación diofantina cuadrática a2+b2=c2{displaystyle a^{2}+b^{2}=c^{2}} ^[1]​ . La nomenclatura se liga al teorema de Pitágoras, el cual afirma que en cualquier triángulo rectángulo, se cumple que r2+s2=t2{displaystyle r^{2}+s^{2}=t^{2}} (donde t es la longitud de la hipotenusa; y las otras variables , longitudes de catetos, en números enteros).En sentido recíproco también se cumple, o sea, cualquier terna pitagórica se puede asociar con las longitudes de los dos catetos y de la hipotenusa correspondiente, formando un triángulo rectángulo.

Definición

A los números enteros u,v,w,{displaystyle u,v,w,} que satisfacen la ecuación diofantina de segundo grado u2+v2=w2{displaystyle u^{2}+v^{2}=w^{2}} , se les llama números pitagóricos ^[2]​

Ternas pitagóricas primitivas

Las ternas pitagóricas suelen representarse como (a,b,c). Las ternas cuyos tres números son primos relativos son denominados ternas pitagóricas primitivas o números pitagóricos. Las 16 primeras ternas pitagóricas primitivas, con c ≤ 100 son:

Historia

Desde un punto de vista histórico, Pitágoras (580- 500 A.D.) fue quien planteó el problema ligado a la construcción de triángulos rectángulos, cuyos lados fuesen longitudes enteras. En cualquier caso, se proponía resolver la ecuación:

a2+b2=c2{displaystyle a^{2}+b^{2}=c^{2}}

para valores enteros de a,b,c{displaystyle a,b,c}. Pitágoras encontró infinitas soluciones al problema en la forma de tres ecuaciones

{a=j2−1b=2jc=j2+1{displaystyle {begin{cases}a&=j^{2}-1\b&=2j\c&=j^{2}+1end{cases}}}

dependientes del parámetro entero positivo j, ^[3]​ como puede ser el ejemplo 82+152=172{displaystyle 8^{2}+15^{2}=17^{2}}.

Por otra parte se atribuye a los babilonios en ser los primeros que encontraron ternas pitagóricas, las cuales están registradas en la tablilla Plimpton 322, algunos investigadores suponen que para generar dichas ternas utilizaron la fórmula:^[4]​

{a=m2−n2b=2mnc=m2+n2{displaystyle {begin{cases}a&=m^{2}-n^{2}\b&=2mn\c&=m^{2}+n^{2}end{cases}}}

como m>n, la cual también aparece en el libro décimo de Los Elementos de Euclides.

Generación y características

Distribución de ternas pitagóricas sobre R+2{displaystyle textstyle mathbb {R} _{+}^{2}}. Los puntos rojos representan aquellas ternas que son primitivas. Los puntos azules son ternas proporcionales a una terna primitiva.

Las ternas pitagóricas pueden clasificarse de dos maneras: primitivas y no primitivas. Una terna pitagórica primitiva es aquella en la que el máximo común divisor de a, b y c es 1. Si (a, b, c) es una terna pitagórica primitiva, se pueden construir infinitas ternas pitagóricas no primitivas (da, db, dc), donde d es un entero positivo. Los triángulos que se construyen con una terna pitagórica no primitiva son siempre proporcionales a otro triángulo cuyos lados forman una terna pitagórica primitiva.

Si m > n son enteros positivos, entonces:

a = m² − n²

b = 2mn

c = m² + n²

es una terna pitagórica. Es primitiva si y sólo si m y n son coprimos y solamente uno de ellos es par (si ambos n y m son impares, entonces a, b y c serán pares, y la terna no será una terna pitagórica primitiva). No todas las ternas pitagóricas pueden ser generadas con las expresiones anteriores, pero todas las ternas primitivas surgen de este modo de un único par de números coprimos m > n. Así pues, existe un número infinito de ternas pitagóricas primitivas.

Si representamos en un plano los puntos que cumplen las condiciones para ser una terna pitagórica, obtenemos el siguiente patrón de puntos (véase imagen de la derecha). Los puntos rojos representan las ternas primitivas y los puntos azules aquellas ternas que no lo son. Como se observa la imagen tiene un eje de simetría debido a que es posible intercambiar a por b y viceversa y obtendremos de nuevo otra terna pitagórica.

Es interesante hacer notar que existe más de una terna primitiva con el mismo número entero menor. El primer ejemplo de esto es el 20, el cual es el menor entero de dos ternas primitivas: (20, 21, 29) y (20, 99, 101).

Generalizaciones

Cuádruplas

Es posible expresar un cuadrado perfecto como la suma de tres cuadrados perfectos, utilizando la siguiente fórmula:^[5]​

(m2+n2+p2)2=(m2+n2−p2)2+(2mp)2+(2np)2{displaystyle (m^{2}+n^{2}+p^{2})^{2}=(m^{2}+n^{2}-p^{2})^{2}+(2mp)^{2}+(2np)^{2}}

Puede ser usada para hallar la diagonal de un paralelepípedo rectangular de dimensiones, dadas en números enteros.

Ejemplos de esto pueden ser:

32=22+22+12{displaystyle 3^{2}=2^{2}+2^{2}+1^{2}}

132=32+42+122{displaystyle 13^{2}=3^{2}+4^{2}+12^{2}}

Último teorema de Fermat

El último teorema de Fermat, postulado por Pierre de Fermat alrededor de 1637, plantea que no existen ternas no triviales análogas a las ternas pitagóricas con números naturales, generalizando para exponentes mayores que dos. En notación moderna, la ecuación:

xn+yn=zn{displaystyle x^{n}+y^{n}=z^{n}}

no tiene solución si n>2 con x, y, z, n naturales.

Sin demostración durante más de 300 años, Andrew Wiles consiguió demostrarlo en 1995, utilizando para ello herramientas matemáticas muy avanzadas de diversas ramas.

Véase también

• Teorema de Pitágoras


• Número primo pitagórico


• Último teorema de Fermat

Referencias

Enlaces externos

• 
  Wikimedia Commons alberga una categoría multimedia sobre Terna pitagórica.


• 
  Weisstein, Eric W. «Pythagorean Triple». En Weisstein, Eric W. MathWorld (en inglés). Wolfram Research.  Plantea una extensa discusión sobre las ternas pitagóricas.


• Ternas-pitagoricas-larsa


• 
  https://web.archive.org/web/20050404113827/http://www.math.clemson.edu/~rsimms/neat/math/pyth/ posee una calculadora Javascript con las fórmulas (m² − n², 2mn, m² + n²) y como se llegan a ellas (en inglés).


• http://www.monografias.com/trabajos5/numelem/numelem.shtml?monosearch


• Tabla de ternas pitagóricas