Csdrhrt

Animación de dos objetos orbitando alrededor de un centro de masas común.

En física, una órbita es la trayectoria que describe un objeto físico alrededor de otro mientras está bajo la influencia de una fuerza central, como la fuerza gravitatoria.

Historia

Se inicia con la aportación matemática de Johannes Kepler, quien fue el que formuló los resultados en sus tres leyes del movimiento planetario. La primera, encontró que las órbitas de los planetas en el sistema solar son elípticas y no circulares o epiciclos, como se pensaba antes, y que el Sol no se encontraba en el centro de sus órbitas sino en uno de sus focos. La segunda, que la velocidad orbital de cada planeta no es constante, como también se creía, sino que la velocidad del planeta depende de la distancia entre el planeta y el Sol .^[1]​ Y la tercera, Kepler encontró una relación universal entre las propiedades orbitales de todos los planetas orbitando alrededor del Sol. Para cada planeta, la distancia entre el planeta y el Sol al cubo, medida en unidades astronómicas, es igual al periodo del planeta al cuadrado, medido en años terrestres.

Isaac Newton demostró que las leyes de Johannes Kepler se derivaban de su teoría de la gravedad y que, en general, las órbitas de los cuerpos que respondían a la fuerza gravitatoria eran secciones cónicas. Isaac Newton demostró que un par de cuerpos siguen órbitas de dimensiones que son inversamente proporcionales a sus masas sobre su centro de masas común. Cuando un cuerpo es mucho más masivo que el otro, se hace la convención de tomar el centro de masas como el centro del cuerpo con mayor masa.

Órbitas planetarias

Órbitas planetarias de Mercurio, Venus, Tierra y Marte.

Dentro de un sistema planetario, los planetas, planetas enanos, asteroides, cometas y la basura espacial orbitan alrededor de la estrella central, el sol, con órbitas elípticas. Un cometa en una órbita parabólica o hiperbólica alrededor de una estrella central no tiene un lazo gravitatorio con la estrella y por tanto no se considera parte del sistema planetario de la estrella. No se han observado en el Sistema Solar cometas con órbitas claramente hiperbólicas. Los cuerpos que tienen un lazo gravitacional con uno de los planetas del sistema planetario, ya sean naturales o artificiales, realizan órbitas elípticas alrededor del planeta.

Debido a las perturbaciones gravitatorias mutuas, las excentricidades de las órbitas de los planetas varían a lo largo del tiempo. Mercurio, el planeta más pequeño del Sistema Solar, tiene la órbita más excéntrica. El siguiente es Marte, mientras que los planetas con menor excentricidad son Venus y Neptuno.

Cuando dos objetos orbitan sobre sí, el periastro es el punto en el que los dos objetos se encuentran más próximos el uno al otro y el apoastro es el punto donde se encuentran más lejos.

En una órbita elíptica, el centro de masas de un sistema entre orbitador y orbitado se sitúa en uno de los focos de ambas órbitas, sin nada en el otro foco. Cuando un planeta se acerca a su periastro, el planeta incrementa su velocidad. De igual manera, cuando se acerca a su apoastro, disminuye su velocidad.

Explicación intuitiva

Hay varias maneras de poder explicar el funcionamiento de una órbita:

• Cuando un objeto se mueve de forma oblicua, cae hacia un objeto orbitado. Sin embargo se mueve tan rápido que la curvatura del objeto orbitado siempre caerá debajo de este.


• Una fuerza, como la gravedad, atrae un objeto hacia una trayectoria curvada mientras intenta mantener el vuelo en línea recta.


• Cuando un objeto cae, se mueve de forma lateral lo suficientemente rápido (tiene suficiente velocidad tangencial) como para evitar el objeto orbitado.

Esquema del cañón de Newton.

Un ejemplo utilizado comúnmente para ilustrar una órbita alrededor de un planeta es el cañón de Newton. Se imagina un cañón situado en lo alto de una montaña que dispara bolas de cañón de forma horizontal. La montaña necesita ser muy alta para evitar la atmósfera terrestre e ignorar los efectos de fricción sobre la bola de cañón.

Si el cañón dispara una bola con una velocidad inicial baja, la trayectoria de la bola se curva e impacta contra el suelo (A). Aumentando la velocidad inicial, la bola de cañón impacta en el suelo cada vez más lejos (B) del cañón, debido a que mientras la bola sigue cayendo, el suelo también se curva. Todos estos movimientos son realmente órbitas en su sentido técnico, ya que describen una trayectoria elíptica alrededor de un centro de gravedad pero que se interrumpe al chocar contra la tierra.

Si se dispara la bola con suficiente velocidad, el suelo se curva al menos tanto como la bola al caer, por lo que la bola de cañón nunca impacta contra el suelo. Se dice que está realizando una órbita sin interrupción o de circunnavegación. Para cada altura sobre el centro de gravedad hay una velocidad específica que produce una órbita circular (C).

Si la velocidad de disparo aumenta más allá de esta velocidad, se producen órbitas elípticas (D). A una velocidad mayor, denominada velocidad de escape, que de nuevo depende de la altura donde se dispara, se produce una órbita infinita (E), primero del tipo parabólica y con velocidades más altas del tipo hiperbólica. En ambos tipos de órbitas infinitas el resultado es que el objeto ha escapado de la gravedad del planeta y se marcha hacia el espacio.

Análisis del movimiento orbital

Tipos de órbitas terrestres.

Teoría clásica de Newton

Para un sistema de solo dos cuerpos que se influyen únicamente por la gravedad, sus órbitas pueden ser calculadas mediante las leyes del movimiento de Newton y la ley de la gravitación universal: la suma de las fuerzas será igual a la masa por su aceleración; la gravedad es proporcional al producto de las masas e inversamente proporcional al cuadrado de la distancia (este cálculo desprecia pequeños efectos como la forma y dimensiones de los cuerpos, que no son relevantes si los cuerpos orbitan a distancias razonablemente grandes comparadas con sus propias dimensiones, y asimismo se ignoran efectos relativistas también muy pequeños en las circunstancias habituales del Sistema Solar).

Para realizar los cálculos, es conveniente describir el movimiento en un sistema de coordenadas que esté enfocado en centro de gravedad del sistema. Si uno de los cuerpos es mucho más masivo que el otro, el centro de gravedad prácticamente coincidirá con el centro del cuerpo más pesado, por lo que se puede decir que el cuerpo más ligero orbita alrededor el más pesado. La teoría newtoniana predice que en un problema de dos cuerpos, la órbita de un cuerpo es una sección cónica. La órbita puede ser abierta, si el objeto nunca regresa, o cerrada, si regresa, dependiendo de la suma total de energía cinética y potencial del sistema. En el caso de una órbita abierta, la velocidad en cualquier posición de la órbita es al menos la de la velocidad de escape para esa posición; en una órbita cerrada, es siempre menor.

Una órbita abierta tiene forma de hipérbola si la velocidad es mayor que la velocidad de escape, o de parábola, si la velocidad es exactamente igual a la velocidad de escape. Los cuerpos se aproximan durante un momento, luego sus trayectorias se curvan una respecto a la otra en el momento que su aproximación es la más cercana y luego se separan para siempre.

Una órbita cerrada tiene forma de elipse. En el caso especial de que el cuerpo orbitante se encuentre siempre a la misma distancia del centro, también tiene forma de círculo. De otra manera, el punto donde el objeto se encuentra más cerca de la Tierra se denomina perigeo, o periastro cuando orbita alrededor de otro cuerpo que no es la Tierra. De forma similar, el punto en el que se encuentra más alejado de la Tierra se llama apogeo, o apoastro si no orbita sobre la Tierra. Una línea dibujada desde el periastro al apoastro es la línea de los ápsides: este es el eje mayor de la elipse.

Los cuerpos orbitantes en órbitas cerradas repiten su trayectoria en un período constante. Este movimiento es descrito por las leyes empíricas de Kepler, que pueden ser derivadas matemáticamente desde las Leyes de Newton. Estas leyes son:

1. La órbita de un planeta alrededor del Sol es una elipse, con el Sol en uno de sus focos. Por tanto, la órbita yace en un plano, denominado plano orbital. El punto de la órbita más cercano al cuerpo atrayente es el periastro. El punto más alejado se denomina apoastro. Existen nombres específicos para cuerpos determinados: los objetos que orbitan alrededor del Sol tienen perihelio y afelio, los objetos que orbitan alrededor de la Tierra tienen perigeo y apogeo.


2. Mientras los planetas se mueven alrededor de su órbita durante una cantidad de tiempo fija, la línea desde el Sol al planeta barre un área constante del plano orbital, sin importar en qué parte de la órbita se encuentra el planeta en ese período. Esto significa que un planeta se mueve más rápido cuando se acerca a su perihelio que cuando lo hace a su afelio, debido a que en la distancia menor se necesita barrer un arco mayor para cubrir el mismo área. La ley se suele resumir como "áreas iguales a tiempos iguales".


3. Para cada planeta, la relación entre el cubo de su semieje mayor con respecto al cuadrado del período es un valor constante para todos los planetas.

Excepto para casos especiales como los puntos de Lagrange, no se conoce un método para solucionar las ecuaciones de movimiento para un sistema de cuatro o más cuerpos. Las soluciones para dos cuerpos se publicaron en los Philosophiae Naturalis Principia Mathematica de I. Newton en 1687. En 1912, Karl F. Sundman desarrolló una serie infinita convergente que soluciona el problema con tres cuerpos, sin embargo su convergencia es demasiado lenta para ser utilizada como método práctico de cálculo. En su lugar, las órbitas pueden ser aproximadas con una precisión alta arbitraria. Existen dos formas para estas aproximaciones.

Una forma es tomar el movimiento elíptico puro como base y añadirle las perturbaciones para tener en cuenta la influencia gravitacional de los otros cuerpos. Este es el método conveniente para calcular las posiciones de objetos astronómicos. Las ecuaciones de movimiento de la Luna, los planetas y otros cuerpos se conocen con gran precisión y se utilizan para generar tablas para la navegación astronómica. Aun así, hay fenómenos seculares que deben ser tratados con métodos post-Newtonianos.

Para propósitos científicos o de una misión espacial, se utiliza la forma de ecuación diferencial. De acuerdo a las Leyes de Newton, la suma de todas las fuerzas es igual a la masa por su aceleración. Por tanto, las aceleraciones se pueden expresar en términos de posición. Los términos de las perturbaciones son más fáciles de describir de esta forma. La predicción de las posiciones futuras y velocidades desde los términos iniciales se soluciona con un problema de valor inicial. Los métodos numéricos calculan las posiciones y velocidades de los objetos para un tiempo futuro muy pequeño, y luego se prolonga repitiéndolo. Sin embargo, los pequeños errores aritméticos debido a la limitada precisión de la matemática del computador se acumulan, limitando la precisión de esta aproximación.

Las simulaciones de diferenciales con grandes cantidades de objetos realizan los cálculos de forma jerárquica entre los centros de masas. Utilizando este esquema se pueden simular galaxias, cúmulos estelares y otros objetos grandes.

Teoría relativista de Einstein

Es bien conocido que la teoría de la relatividad especial está en contradicción con la teoría newtoniana de la gravitación, ya que en esta tiene lugar la acción a distancia instantánea. Esa y otras razones llevaron a Einstein a buscar una teoría más general que fue la teoría de la relatividad general que incorpora una descripción relativista adecuada del campo gravitatorio. En esta teoría la presencia de una masa en el espacio curva el espacio-tiempo de tal manera que la geometría del mismo deja de ser euclidiana (aunque sigue siendo aproximadamente euclídea si las masas y velocidades de los cuerpos toman valores como los observados en el sistema solar). Las órbitas planetarias no son estrictamente secciones cónicas sino curvas geodésicas (líneas de mínima curvatura) sobre la geometría curva del espacio-tiempo. La teoría es no lineal y resulta muy complicado hacer cálculos por ejemplo para un problema de dos cuerpos de masas iguales. Sin embargo, para sistemas planetarios como el sistema solar, en que el astro central, el sol, es mucho más masivo que el resto de planetas, puede estimarse la curvatura del espacio-tiempo debida únicamente al sol (despreciando la del resto de planetas) y asumir que los planetas mucho menos masivos se mueven según geodésicas de la geometría curvada por el sol.

Para los valores presentes en el sistema solar los resultados cuantitativos de la teoría einsteniana son numéricamente muy cercanos a la teoría newtoniana (por lo que generalmente se justifica a efectos prácticos usar la teoría newtoniana que es computacionalmente más simple). Sin embargo, la teoría newtoniana no puede explicar algunos hechos que sí son correctamente explicados por teoría relativista de Einstein, entre los que se encuentra el notable efecto de avance del perihelio del planeta Mercurio, que es explicado con muy buena aproximación por la teoría relativista de Einstein pero no por la teoría newtoniana.

Órbitas en el caso newtoniano

Para analizar el movimiento de un cuerpo bajo la influencia de una fuerza que siempre se dirige desde un punto fijo es conveniente utilizar coordenadas polares cuyo origen coincida con el centro de la fuerza. En tal sistema de coordenadas, sus componentes radial y transversal son respectivamente:

ar=d2rdt2−r(dθdt)2{displaystyle a_{r}={frac {d^{2}r}{dt^{2}}}-rleft({frac {dtheta }{dt}}right)^{2}}

aθ=1rddt(r2dθdt){displaystyle a_{theta }={frac {1}{r}}{frac {d}{dt}}left(r^{2}{frac {dtheta }{dt}}right)}

Ya que la fuerza es completamente radial y que la aceleración es proporcional a la fuerza, implica que la aceleración transversal es igual a cero. Como resultado,

ddt(r2dθdt)=0{displaystyle {frac {d}{dt}}left(r^{2}{frac {dtheta }{dt}}right)=0}.

Tras su integración, se obtiene,

r2dθdt=const.{displaystyle r^{2}{frac {dtheta }{dt}}={rm {const.}}}, que es una prueba teórica de la segunda ley de Kepler.

La constante de integración l es el momento angular por unidad de masa. Por tanto,

dθdt=lr2=lu2{displaystyle {frac {dtheta }{dt}}={l over r^{2}}=lu^{2}}

Donde se introduce una variable adicional,

u=1r{displaystyle u={1 over r}}

La fuerza radial es f(r) por unidad es ar{displaystyle a_{r}}, tras la eliminación la variable tiempo del componente radial de la ecuación se obtiene,

d2udθ2+u=−f(1/u)l2u2{displaystyle {frac {d^{2}u}{dtheta ^{2}}}+u=-{frac {f(1/u)}{l^{2}u^{2}}}}

En el caso de la gravedad, la ley universal de gravitación de Newton afirma que la fuerza es inversamente proporcional al cuadrado de la distancia,

f(1/u)=ar=−GMr2=−GMu2{displaystyle f(1/u)=a_{r}={-GM over r^{2}}=-GMu^{2}}

Donde G es la constante de gravitación universal, m la masa del cuerpo orbitante y M la masa del cuerpo central. Sustituyendo en la ecuación anterior se obtiene,

d2udθ2+u=GMl2{displaystyle {frac {d^{2}u}{dtheta ^{2}}}+u={frac {GM}{l^{2}}}}

Para la fuerza gravitacional, el término de la derecha de la ecuación se convierte en una constante y la ecuación se parece a una ecuación armónica. La ecuación para la órbita descrita por la partícula es:

r=1u=l2/GM1+ecos⁡(θ−θ0)=p1+ecos⁡(θ−θ0){displaystyle r={frac {1}{u}}={frac {l^{2}/GM}{1+ecos(theta -theta _{0})}}={frac {p}{1+ecos(theta -theta _{0})}}}

Donde p, e y θ0{displaystyle theta _{0}} son constantes de la integración,

p=l2GM=a(1−e2){displaystyle p={l^{2} over GM}=a(1-e^{2})}

Si el parámetro e es menor que uno, e es la excentricidad y a es el semieje mayor para una elipse. En general, se puede reconocer como la ecuación de una sección cónica en coordenadas polares (r,θ).

Órbitas en el caso relativista

En el caso relativista, el problema de dos cuerpos puede resolverse aproximadamente usando la solución de Schwarzschild para el campo gravitatorio creado por un cuerpo con simetría esférica. La órbita planteria en el espacio-tiempo es una geodésica de la métrica de Schwarzschild. La órbita así obtenida obtendría a partir de una geodésica de la métrica de métrica de Schwarzschild es equivalente a que la partícula notara una aceleración radial efectiva dada por:

ar=GM(1r2+3l2c2r4){displaystyle a_{r}=GMleft({frac {1}{r^{2}}}+{frac {3l^{2}}{c^{2}r^{4}}}right)}

donde:

G,c{displaystyle G,c,}, constante de la gravitación universal y velocidad de la luz.

r{displaystyle r,}, coordenada radial de Schwarzschild.

l{displaystyle l,}, momento angular orbital del planeta por unidad de masa.

Las constantes del movimiento asociadas a la energía y el momento angular son:

12(r˙2+r2θ˙2)−GM(1r2+3l2c2r4)=E,r2θ˙=l{displaystyle {frac {1}{2}}left({dot {r}}^{2}+r^{2}{dot {theta }}^{2}right)-GMleft({frac {1}{r^{2}}}+{frac {3l^{2}}{c^{2}r^{4}}}right)=E,qquad r^{2}{dot {theta }}=l}

La ecuación del movimiento, haciendo el cambio u=1/r{displaystyle u=1/r,} como en el caso clásico, queda como:

(dudθ)2=2GMl2u−u2+2GMc2u3+2El2{displaystyle left({frac {mathrm {d} u}{mathrm {d} theta }}right)^{2}={frac {2GM}{l^{2}}}u-u^{2}+{frac {2GM}{c^{2}}}u^{3}+{frac {2E}{l^{2}}}}

Para todos los planetas del sistema solar la corrección relativista dada por el tercer término del segundo miembro es pequeña comparada con los otros términos. Para mostrar esto conviene introducir un parámetro adimensional ϵ=2(GM/cl)2{displaystyle epsilon =2(GM/cl)^{2}} y hacer un nuevo cambio de variable u¯=ul2/GM{displaystyle {bar {u}}=ul^{2}/GM} con lo que la ecuación de movimiento puede reescribirse como:

(*)(du¯dθ)2=2u¯−u¯2+ϵu¯3−β=:f(u¯){displaystyle left({frac {mathrm {d} {bar {u}}}{mathrm {d} theta }}right)^{2}=2{bar {u}}-{bar {u}}^{2}+epsilon {bar {u}}^{3}-beta =:f({bar {u}})}

donde:

β:=−2El2G2M2=1−e2{displaystyle beta :=-{frac {2El^{2}}{G^{2}M^{2}}}=1-e^{2}}

Para el planeta Mercurio el parámetro ϵ{displaystyle epsilon } es máximo, alcanzado el valor ϵ=5,09⋅10−8{displaystyle epsilon =5,09cdot 10^{-8}}. Sin embargo, la pequeñez de este término hace que las correcciones relativistas produzcan solo pequeñas correcciones y por esa razón la teoría newtoniana da tan buenas aproximaciones para el sistema solar. Buscando las raíces de la función f(u¯){displaystyle f({bar {u}})}, teniendo en cuenta la pequeñez de este parámetro, se llega a:

{u¯1=1−e−ϵ2e(1−e)3+O(ϵ2)u¯2=1+e+ϵ2e(1+e)3+O(ϵ2)u¯3=1α−2+O(ϵ){displaystyle {begin{cases}{bar {u}}_{1}=1-e-{cfrac {epsilon }{2e}}(1-e)^{3}+O(epsilon ^{2})\{bar {u}}_{2}=1+e+{cfrac {epsilon }{2e}}(1+e)^{3}+O(epsilon ^{2})\{bar {u}}_{3}={cfrac {1}{alpha }}-2+O(epsilon )end{cases}}}

Para las órbitas planetarias estables se tiene u¯1<u¯<u¯2{displaystyle {bar {u}}_{1}<{bar {u}}<{bar {u}}_{2}} (el caso u>u¯3{displaystyle u>{bar {u}}_{3}} queda excluido ya que implica que la partícula cae sobre el sol u¯→∞{displaystyle {bar {u}}to infty }). La solución de la ecuación (*) viene dada por:

ϵ1/2θ=∫dv(v−u¯1)(v−u¯2)(v−u¯3){displaystyle epsilon ^{1/2}theta =int {frac {mathrm {d} v}{sqrt {(v-{bar {u}}_{1})(v-{bar {u}}_{2})(v-{bar {u}}_{3})}}}}

Esta integral puede reducirse a una integral elíptica mediante el cambio de variable v=u¯1+1/t2{displaystyle v={bar {u}}_{1}+1/t^{2}}, quedando como:

(**)ϵ1/2θ=−2ab∫dt(t2−a2)(t2−b2){displaystyle epsilon ^{1/2}theta =-2abint {frac {mathrm {d} t}{sqrt {(t^{2}-a^{2})(t^{2}-b^{2})}}}}

donde:

a2=1/(u¯2−u¯1),b2=1/(u¯3−u¯1){displaystyle a^{2}=1/({bar {u}}_{2}-{bar {u}}_{1}),quad b^{2}=1/({bar {u}}_{3}-{bar {u}}_{1})}

Usando una de las funciones elípticas de Jacobi la integral (**) se puede integrar como:

ϵ1/2θ=b ns−1(t/a){displaystyle epsilon ^{1/2}theta =b mathrm {ns} ^{-1}(t/a)}

con módulo dado por k=b/a{displaystyle k={sqrt {b/a}}}, usando este resultado par ala ecuación de la órbita se tiene:

(***)u¯=u¯1+(u¯2−u¯1)sn2(12ϵ(u¯3−u¯1)θ)⇒1r=GMl2(A+Bsn2(ηθ)){displaystyle {bar {u}}={bar {u}}_{1}+({bar {u}}_{2}-{bar {u}}_{1})mathrm {sn} ^{2}left({frac {1}{2}}{sqrt {epsilon ({bar {u}}_{3}-{bar {u}}_{1})}}theta right)Rightarrow quad {frac {1}{r}}={frac {GM}{l^{2}}}(A+Bmathrm {sn} ^{2}(eta theta ))}

donde:

A=1−e−ϵ2e(1−e)3+O(ϵ2){displaystyle A=1-e-{frac {epsilon }{2e}}(1-e)^{3}+O(epsilon ^{2})}

B=2e+ϵ(3e+1/e)+O(ϵ2){displaystyle B=2e+epsilon (3e+1/e)+O(epsilon ^{2})}

η=12−(3−e)ϵ4+O(ϵ2){displaystyle eta ={frac {1}{2}}-{frac {(3-e)epsilon }{4}}+O(epsilon ^{2})}

k2=2eϵ+O(ϵ2){displaystyle k^{2}=2eepsilon +O(epsilon ^{2})}, es el módulo de las función elíptica de Jacobi para la órbita.

Si ϵ=0{displaystyle epsilon =0}, entonces A=1−e,B=2e,η=1/2,k=0{displaystyle A=1-e,B=2e,eta =1/2,k=0} y en ese caso la órbita queda reducida al caso newtoniano clásico:

l2GMr=1−ecos⁡θ{displaystyle {frac {l^{2}}{GMr}}=1-ecos theta }

Que es una elipse de excentricidad e. La órbita relativista sin embargo no es periódica es una cuasi-elipse que gira lentamente alrededor del sol. Esto se conoce como avance del perihelio que es más acusado para el planeta Mercurio. A partir de la solución (***) el perihelio aparece en θ=K/η{displaystyle theta =K/eta } y el siguiente valor para el que se da es θ=3K/η{displaystyle theta =3K/eta } (donde K es un cuarto del período, dado por la integral elíptica de primera especie completa), por lo tanto entre dos perihelios el ángulo girado no es 2π{displaystyle 2pi } sino una cantidad ligeramente mayor:

2Kη=2π+π(1+14k2+…)12−14(3−ϵ)≈2π+3πϵ{displaystyle {frac {2K}{eta }}=2pi +{frac {pi (1+{frac {1}{4}}k^{2}+dots )}{{frac {1}{2}}-{frac {1}{4}}(3-epsilon )}}approx 2pi +3pi epsilon }

Para Mercurio con ϵ=5,09⋅10−8{displaystyle epsilon =5,09cdot 10^{-8}} el avance del perihelio predicho es de 41.07″/siglo{displaystyle 41.07''/mathrm {siglo} } (siendo su período de 88 días), que es prácticamente el valor experimental 42.98″/siglo{displaystyle 42.98''/mathrm {siglo} }. Este gran acuerdo constituyó uno de los éxitos iniciales de la teoría que le dio gran aceptación general.

Período orbital

El período orbital es el tiempo que tarda un planeta u otro objeto en realizar una órbita completa. Existen varios tipos de períodos orbitales para los objetos alrededor del Sol:

• El período sidéreo es el tiempo que tarda el objeto en dar una órbita completa alrededor del Sol, respecto de las estrellas. Se considera como el período orbital verdadero del objeto.


• El período sinódico es el tiempo que tarda el objeto en reaparecer en el mismo punto del cielo, respecto al Sol, cuando es observado desde la Tierra. Este período comprende el tiempo entre dos conjunciones sucesivas y es el período orbital aparante del objeto. El período sinódico difiere del sidéreo porque la Tierra también gira alrededor del Sol.


• El período draconítico es el tiempo que tarda en pasar dos veces el objeto por su nodo ascendente, el punto de su órbita que cruza la eclíptica desde el hemisferio sur al norte. Se diferencia del período sidéreo porque la línea de nodos suele variar lentamente.


• El período anomalístico es el tiempo que tarda en pasar dos veces el objeto por su perihelio, el punto más próximo al Sol. Se diferencia del período sidéreo porque el semieje mayor también suele variar lentamente.


• El período tropical es el tiempo que tarda en pasar dos veces el objeto por la ascensión recta de cero. Es ligeramente más corto que el período sidéreo debido a la precesión de los equinoccios.

Parámetros geométricos de la órbita

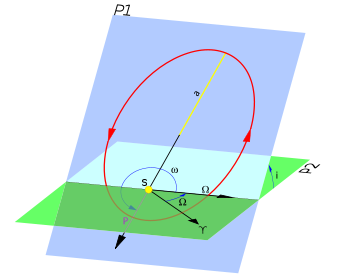
Elementos orbitales de un cuerpo alrededor del Sol.

Los elementos orbitales son los parámetros necesarios para especificar una órbita, utilizando un modelo de dos masas obedeciendo las leyes de movimiento de Newton. Existe seis parámetros básicos, también denominados elementos keplerianos en honor a Kepler:

• 
  Longitud del nodo ascendente (Ω{displaystyle Omega ,!}) .


• 
  Inclinación(i{displaystyle i,!}).


• 
  Argumento del perihelio (ω{displaystyle omega ,!}).


• 
  Semieje mayor (a{displaystyle a,!}).


• 
  Excentricidad (e{displaystyle e,!}).


• 
  Anomalía media de la época (Mo{displaystyle M_{o},!}).

Además, otros elementos orbitales son: anomalía verdadera (v{displaystyle v,}), semieje menor (b{displaystyle b,}), excentricidad linear (ϵ{displaystyle epsilon ,}), anomalía excéntrica (E{displaystyle E,}), longitud media (L{displaystyle L,}), longitud verdadera (l{displaystyle l,}) y período orbital (T{displaystyle T,}).

Tipos de órbitas

Por características

Por cuerpo central

Órbitas terrestres

• 
  Órbita geocéntrica
  
  
  
  • 
    Órbita geosíncrona
    
    
    
    • Órbita geoestacionaria
    
    
    • Órbita de transferencia geoestacionaria
    
    
    
    
  
  
  • Órbita baja terrestre
  
  
  • Órbita media terrestre
  
  
  • Órbita de Molniya
  
  
  • Órbita casi ecuatorial
  
  
  • Órbita de la Luna
  
  
  • Órbita polar
  
  
  • Órbita heliosíncrona
  
  
  • Órbita tundra
  
  
  
  

Órbitas marcianas

• 
  Órbita areosíncrona
  
  • Órbita areoestacionaria
  
  

Órbitas lunares

• Órbita lunar

Órbitas solares

• Órbita heliocéntrica

Véase también

• Asistencia gravitatoria


• Exponente Lyapunov


• Trayectoria


• Velocidad orbital


• Vector Excentricidad

Referencias

Bibliografía

• 
  Abell, Morrison, and Wolff (1987). Exploration of the Universe (5ª Ed. edición). Saunders College Publishing. 
  


• 
  Ortega, Manuel R. (1989-2010). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7. 
  


• “Rumbo al Cosmos. Los secretos de la astronáutica”

Enlaces externos

• 
  Orbital Mechanics (en inglés)


• 
  Motion under different kinds of force (requiere Java)


• 
  ¡Dispara una bola de cañón en órbita!, animación del cañón de Newton (requiere Flash)


• Animación interactiva de formas de órbitas