Csdrhrt

En matemáticas, los armónicos esféricos son funciones armónicas que representan la variación espacial de un conjunto ortogonal de soluciones de la ecuación de Laplace cuando la solución se expresa en coordenadas esféricas.

Los armónicos esféricos son importantes en muchas aplicaciones teóricas y prácticas, en particular en la física atómica (dado que la función de onda de los electrones contiene armónicos esféricos) y en la teoría del potencial, que resulta relevante tanto para el campo gravitatorio como para la electrostática.

Introducción

La ecuación de Laplace en coordenadas esféricas viene dada por:

∇2f=1r2∂∂r(r2∂f∂r)+1r2sin⁡θ∂∂θ(sin⁡θ∂f∂θ)+1r2sin2⁡θ∂2f∂φ2=0{displaystyle nabla ^{2}f={1 over r^{2}}{partial over partial r}left(r^{2}{partial f over partial r}right)+{1 over r^{2}sin theta }{partial over partial theta }left(sin theta {partial f over partial theta }right)+{1 over r^{2}sin ^{2}theta }{partial ^{2}f over partial varphi ^{2}}=0}

(véase también nabla y laplaciano en coordenadas esféricas). Si en esta expresión se consideran soluciones particulares de la forma, f(r,θ,ϕ)=R(r)Y(θ,φ){displaystyle f(r,theta ,phi )=R(r)Y(theta ,varphi )}, la parte angular Y, se le denomina armónico esférico y satisface la relación:

1sin⁡θ∂∂θ(sin⁡θ∂Y(θ,φ)∂θ)+1sin2⁡θ∂2Y(θ,φ)∂φ2+l(l+1)Y(θ,φ)=0{displaystyle {1 over sin theta }{partial over partial theta }left(sin theta {partial Y(theta ,varphi ) over partial theta }right)+{1 over sin ^{2}theta }{partial ^{2}Y(theta ,varphi ) over partial varphi ^{2}}+l(l+1)Y(theta ,varphi )=0}

Si a su vez se usa el método de separación de variables a esta última ecuación se puede ver que la ecuación anterior admite soluciones periódicas en las dos coordenadas angulares l es un número entero. Entonces la solución periódica del sistema anterior dependerá de los dos enteros (l, m) y vendrá dada en términos de funciones trigonométricas y de polinomios asociados de Legendre:

Yℓm(θ,φ)=NeimφPℓm(cos⁡θ){displaystyle Y_{ell }^{m}(theta ,varphi )=N,e^{imvarphi },P_{ell }^{m}(cos {theta })},

Donde Yℓm{displaystyle Y_{ell }^{m}} se llama función armónica esférica de grado ℓ{displaystyle ell } y orden m{displaystyle m}, Pℓm{displaystyle P_{ell }^{m}} es el polinomio asociado de Legendre, N{displaystyle N} es una constante de normalización y θ{displaystyle theta } y φ{displaystyle varphi } representan las variables angulares (el ángulo polar o colatitud y azimutal o longitud, respectivamente).

Las coordenadas esféricas utilizadas en este artículo son consistentes con las utilizadas por los físicos, pero difieren de las utilizadas por los matemáticos (ver coordenadas esféricas). En particular, la colatitud θ{displaystyle theta }, o ángulo polar, se encuentra en el rango 0≤θ≤π{displaystyle 0leq theta leq pi } y la longitud φ{displaystyle varphi }, o azimuth, posee el rango 0≤φ<2π{displaystyle 0leq varphi <2pi }. Por lo tanto, θ{displaystyle theta } es 0 en el Polo Norte, π/2{displaystyle pi /2} en el Ecuador, y π{displaystyle pi } en el Polo Sur.

Cuando la ecuación de Laplace se resuelve sobre un dominio esférico, las condiciones de periodicidad sobre la frontera en la coordenada φ{displaystyle varphi } así como las condiciones de regularidad en el "polo norte" y "sur" de la esfera, conllevan como se ha dicho que los números el grado l y el orden m necesarios para que se satisfagan deben ser enteros que cumplen: ℓ≥0{displaystyle ell geq 0} y |m|≤ℓ{displaystyle |m|leq ell }.

Normalización

Existen varias normalizaciones utilizadas para las funciones de armónicos esféricos. En física y sismología estas funciones son generalmente definidas como

Yℓm(θ,φ)=AℓmPℓm(cos⁡θ)eimφ{displaystyle Y_{ell }^{m}(theta ,varphi )=A_{ell }^{m}P_{ell }^{m}(cos {theta }),e^{imvarphi }}

donde

Aℓm=(2ℓ+1)4π(ℓ−m)!(ℓ+m)!{displaystyle A_{ell }^{m}={sqrt {{(2ell +1) over 4pi }{(ell -m)! over (ell +m)!}}}}

Estas funciones están ortonormalizadas

∫02πdφ∫−11d(cos⁡θ)Yℓm(θ,φ∗)Yℓ′m′∗(θ,φ)=δℓℓ′δmm′{displaystyle int _{0}^{2pi }dvarphi int _{-1}^{1}d(cos theta )Y_{ell }^{m}(theta ,varphi ^{*}),Y_{ell '}^{m'*}(theta ,varphi ),=delta _{ell ell '},delta _{mm'}},

donde δ_aa = 1, δ_ab = 0 si a ≠ b, (ver delta de Kronecker). Mientras que en las áreas de geodésica y análisis espectral se utiliza

Yℓm(θ,φ)=(2ℓ+1)(ℓ−m)!(ℓ+m)!Pℓm(cos⁡θ)eimφ{displaystyle Y_{ell }^{m}(theta ,varphi )={sqrt {{(2ell +1)}{(ell -m)! over (ell +m)!}}},P_{ell }^{m}(cos {theta }),e^{imvarphi }}

que posee una potencia unitaria

14π∫02πdφ∫−11d(cos⁡θ)Yℓm(θ,φ∗)Yℓ′m′∗(θ,φ)=δℓℓ′δmm′{displaystyle {1 over 4pi }int _{0}^{2pi }dvarphi int _{-1}^{1}d(cos theta )Y_{ell }^{m}(theta ,varphi ^{*}),Y_{ell '}^{m'*}(theta ,varphi ),=delta _{ell ell '},delta _{mm'}}.

En temas de magnetismo, en cambio, se utilizan los armónicos de Schmidt semi-normalizados

Yℓm(θ,φ)=(2l+1)(ℓ−m)!(ℓ+m)!Pℓm(cos⁡θ)eimφ{displaystyle Y_{ell }^{m}(theta ,varphi )={sqrt {(2l+1){(ell -m)! over (ell +m)!}}}P_{ell }^{m}(cos {theta }),e^{imvarphi }}

poseen la siguiente normalización

∫φ=02π∫−11d(cosθ)Yℓm(θ,φ∗)Yℓ′m′∗(θ,φ)=4π(2ℓ+1)δℓℓ′δmm′{displaystyle int _{varphi =0}^{2pi }int _{-1}^{1}d(costheta )Y_{ell }^{m}(theta ,varphi ^{*}),Y_{ell '}^{m'*}(theta ,varphi ),={4pi over (2ell +1)}delta _{ell ell '},delta _{mm'}}.

Utilizando la identidad (ver Polinomios asociados de Legendre)

Pℓ−m=(−1)m(ℓ−m)!(ℓ+m)!Pℓm{displaystyle P_{ell }^{-m}=(-1)^{m}{frac {(ell -m)!}{(ell +m)!}}P_{ell }^{m}}

se puede demostrar que todas las funciones armónicas esféricas normalizadas mencionadas en los párrafos anteriores satisfacen

Yℓm∗(θ,φ)=(−1)mYℓ−m(θ,φ){displaystyle Y_{ell }^{m*}(theta ,varphi )=(-1)^{m}Y_{ell }^{-m}(theta ,varphi )},

donde el símbolo * significa conjugación compleja.

Convención de fase de Condon-Shortley

Una fuente de confusión con la definición de los esféricos armónicos es el factor de fase de (−1)m{displaystyle (-1)^{m},}, comúnmente identificado como la fase de Condon-Shortley en la literatura relacionada con mecánica cuántica. En el área de mecánica cuántica, es práctica usual incluir este factor de fase en la definición de las funciones asociadas de Legendre, o acoplarlo a la definición de las funciones armónicas esféricas. No existe ningún requerimiento que obligue a utilizar la fase de Condon-Shortley en la definición de las funciones esféricas armónicas pero, si es que se la incluye, entonces algunas operaciones en el campo de la mecánica cuántica son más simples. Por el contrario en los campos de geodesia y magnetismo nunca se incluye el factor de fase de Condon-Shortley en la definición de los esféricos armónicos.

Definición matemática: Armónicos hiperesféricos

En matemáticas se usa una noción de armónico esférico más amplia que en física. Dado un polinomio P(x) homogéneo y armónico de grado m sobre Rn{displaystyle mathbb {R} ^{n}} se denomina armónico esférico de grado m a la función obtenida como restricción de P(x) a la (n-1)-esfera Sn−1⊂Rn{displaystyle S^{n-1}subset mathbb {R} ^{n}}. Las funciones consideradas anteriormente Y(θ,φ){displaystyle Y(theta ,varphi )} son obviamente ejemplos de funciones armónicas, pero también son ciertas combinaciones lineales de los mismos. Para n > 3 la definición anterior permite definir armónicos hiperesféricos, que generalizan la definición a espacios de dimensión superior.

Si Hm(Sn){displaystyle {mathcal {H}}_{m}(S^{n})} designa a todos las funciones armónicas de grado m, se pueden demostrar una serie de propiedades importantes:

1. El espacio de funciones de cuadrado integrable sobre la n-esfera es suma directa de espacios anteriores L2(Sn)=⨁m=0∞Hm(Sn){displaystyle L^{2}(S^{n})=bigoplus _{m=0}^{infty }{mathcal {H}}_{m}(S^{n})}
   


2. Dados dos espacios Hm(Sn){displaystyle {mathcal {H}}_{m}(S^{n})} y Hk(Sn){displaystyle {mathcal {H}}_{k}(S^{n})} con m≠k{displaystyle mneq k}, entonces esos dos espacios son ortogonales.


3. La dimensión del espacio Hm(Sn){displaystyle {mathcal {H}}_{m}(S^{n})} viene dada por:

dim⁡Hm(Sn−1)=(n+m−1n−1)−(n+m−3n−1){displaystyle dim {mathcal {H}}_{m}(S^{n-1})={begin{pmatrix}n+m-1\n-1end{pmatrix}}-{begin{pmatrix}n+m-3\n-1end{pmatrix}}}

Expansión en armónicos esféricos

Los armónicos esféricos forman un conjunto completo ortonormal de funciones y por lo tanto forman un espacio vectorial análogo a vectores unitarios de la base. Sobre la esfera unitaria, toda función de cuadrado integrable puede, por lo tanto, ser expandida como una combinación lineal de:

f(θ,φ)=∑ℓ=0∞∑m=−ℓℓfℓmYℓm(θ,φ){displaystyle f(theta ,varphi )=sum _{ell =0}^{infty }sum _{m=-ell }^{ell }f_{ell }^{m},Y_{ell }^{m}(theta ,varphi )}.

Esta expansión es exacta siempre y cuando ℓ{displaystyle ell } se extienda a infinito. Se producirá un error de truncamiento al limitar la suma sobre ℓ{displaystyle ell } a un ancho de banda finito L{displaystyle L}. Los coeficientes de la expansión fℓm{displaystyle f_{ell }^{m}} pueden obtenerse multiplicando la ecuación precedente por el complejo conjugado de los esféricos armónicos, integrando sobre un ángulo sólido Ω{displaystyle Omega !,}, y utilizando las relaciones de ortogonalidad indicadas previamente. Para el caso de armónicos ortonormalizados, se obtiene

fℓm=∫Ωf(θ,φ)Yℓm∗(θ,φ)dΩ=∫02πdφ∫0πdθsin⁡θf(θ,φ)Yℓm∗(θ,φ){displaystyle f_{ell }^{m}=int _{Omega }f(theta ,varphi ),Y_{ell }^{m*}(theta ,varphi )dOmega =int _{0}^{2pi }dvarphi int _{0}^{pi }dtheta sin theta f(theta ,varphi )Y_{ell }^{m*}(theta ,varphi )}.

Un conjunto alternativo de armónicos esféricos para funciones reales puede ser obtenido a partir del conjunto

Yℓm={Yℓ0 si m=012(Yℓm+(−1)mYℓ−m)=2NPℓm(θ)cos⁡mφsi m>01i2(Yℓ|m|−(−1)|m|Yℓ−|m|)=2NPℓ|m|(θ)sin⁡|m|φ si m<0.{displaystyle Y_{ell m}={begin{cases}Y_{ell }^{0}qquad qquad qquad qquad qquad qquad qquad qquad qquad qquad quad quad {mbox{ si }}m=0\{1 over {sqrt {2}}}left(Y_{ell }^{m}+(-1)^{m},Y_{ell }^{-m}right)={sqrt {2}}NP_{ell }^{m}(theta )cos mvarphi qquad quad quad {mbox{si }}m>0\{1 over i{sqrt {2}}}left(Y_{ell }^{|m|}-(-1)^{|m|},Y_{ell }^{-|m|}right)={sqrt {2}}NP_{ell }^{|m|}(theta )sin |m|varphi quad {mbox{ si }}m<0.end{cases}}}

Estas funciones tienen las mismas propiedades de normalización que las funciones complejas indicadas previamente. En esta notación, una función real integrable puede ser expresada como una suma de armónicos esféricos de infinitos términos como

f(θ,φ)=∑ℓ=0∞∑m=−ℓℓflmYlm(θ,φ){displaystyle f(theta ,varphi )=sum _{ell =0}^{infty }sum _{m=-ell }^{ell }f_{lm},Y_{lm}(theta ,varphi )}.

Armónicos Esféricos en física

A continuación mencionaremos algunas aplicaciones de los armónicos esféricos en física, tanto en electrostática como en mecánica cuántica.

Armónicos esféricos en electrostática

El átomo de hidrógeno

El moderno modelo atómico cuántico del átomo de hidrógeno presupone que cada electrón en un estado estacionario de energía del electrón tiene una posición que se distribuye alrededor del núcleo atómico con una distribución de probabilidad cuya variación angular viene dada por un armónico esférico.

Análisis espectral

La potencia total de una función f{displaystyle f} es definida en la literatura de procesamiento de señales electrónicas como la integral de la función elevada al cuadrado, dividida por el área que abarca. Usando las propiedades de ortonormalidad de las funciones armónicas esféricas de potencia real unitaria, es fácil verificar que la potencia total de una función definida sobre la esfera unitaria se relaciona con sus coeficientes espectrales a través de una generalización del teorema de Parseval:

14π∫Ωf(Ω)2dΩ=∑l=0∞Sff(l){displaystyle {frac {1}{4,pi }}int _{Omega }f(Omega )^{2},dOmega =sum _{l=0}^{infty }S_{f!f}(l)},

donde

Sff(l)=∑m=−llflm2{displaystyle S_{f!f}(l)=sum _{m=-l}^{l}f_{lm}^{2}}

se define como el espectro de potencia angular. En forma similar, se puede definir la potencia cruzada entre dos funciones como

14π∫Ωf(Ω)g(Ω)dΩ=∑l=0∞Sfg(l){displaystyle {frac {1}{4,pi }}int _{Omega }f(Omega ),g(Omega ),dOmega =sum _{l=0}^{infty }S_{fg}(l)},

donde

Sfg(l)=∑m=−llflmglm{displaystyle S_{fg}(l)=sum _{m=-l}^{l}f_{lm}g_{lm}}

se define como el espectro cruzado en este caso. Si las funciones f{displaystyle f} y g{displaystyle g} tienen un valor promedio igual a cero (o sea los coeficientes espectrales f00{displaystyle f_{00}} y g00{displaystyle g_{00}} son nulos), entonces Sff(l){displaystyle S_{f!f}(l)} y Sfg(l){displaystyle S_{fg}(l)} representan las contribuciones a la varianza y covarianza de la función para el grado ℓ{displaystyle ell }, respectivamente. Es común que el espectro de potencia cruzado se pueda aproximar por una power law del tipo

Sff(l)=Cℓβ{displaystyle S_{f!f}(l)=C,ell ^{beta }}.

Cuando β=0{displaystyle beta =0}, el espectro es "blanco" dado que cada grado posee idéntica potencia. Cuando β<0{displaystyle beta <0}, el espectro se denomina "rojo" ya que existe mayor potencia a grados bajos con longitudes de onda largas que a altos grados. Finalmente, cuando β>0{displaystyle beta >0}, el espectro es denominado "azul".

Teorema de la suma

Un resultado matemático de sumo interés y utilidad es el llamado teorema de la suma para los armónicos esféricos. Dos vectores r y r', con coordenadas esféricas (r,θ,φ){displaystyle (r,theta ,varphi )} y (r′,θ′,φ′){displaystyle (r',theta ',varphi ')}, respectivamente, tienen un ángulo γ{displaystyle gamma } entre ellos dado por la expresión

cos⁡γ=cos⁡θcos⁡θ′+sin⁡θsin⁡θ′cos⁡(φ−φ′){displaystyle cos gamma =cos theta cos theta '+sin theta sin theta 'cos(varphi -varphi ')}.

El teorema de la suma expresa un polinomio de Legendre de orden l{displaystyle l} en el ángulo γ{displaystyle gamma } en términos de los productos de dos armónicos esféricos con coordenadas angulares (θ,φ){displaystyle (theta ,varphi )} y (θ′,φ′){displaystyle (theta ',varphi ')}:

Pl(cos⁡γ)=4π2l+1∑m=−llYlm∗(θ′,φ′)Ylm(θ,φ){displaystyle P_{l}(cos gamma )={frac {4pi }{2l+1}}sum _{m=-l}^{l}Y_{lm}^{*}(theta ',varphi '),Y_{lm}(theta ,varphi )}.

Esta expresión es válida tanto para los armónicos reales como para los complejos. Sin embargo, debe enfatizarse que la fórmula indicada previamente es válida solo para armónicos esféricos ortonormalizados. Para armónicos de potencia unitaria es necesario eliminar el factor 4π{displaystyle 4pi } de la expresión anterior.

Visualización de los armónicos esféricos

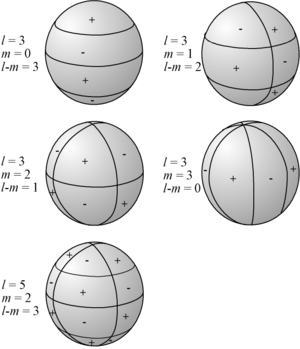
Representación esquemática de Y_lm sobre la esfera unitaria. Y_lm es igual a 0 a lo largo de m círculos que pasan a través de los polos, y a lo largo de l-m círculos de igual latitud. La función cambia de signo cada vez que cruza una de dichas líneas.

La función armónica esférica real Y₃₂ mostrada a lo largo de cuatro cortes.

Los armónicos esféricos son fáciles de visualizar contando el número de cruces por cero que ellos tienen tanto en dirección de las latitudes como de las longitudes. Para la dirección en las latitudes, las funciones asociadas de Legendre tienen l−|m|{displaystyle l-|m|} ceros, mientras que en sentido longitudinal, las funciones trigonometricas seno y coseno tienen 2|m|{displaystyle 2|m|} ceros.

Cuando el armónico esférico de orden m{displaystyle m} es nulo o cero, las funciones armónicas esféricas no dependen de la longitud, y se dice que la función es zonal. Cuando l=|m|{displaystyle l=|m|}, no existen cruces por cero en sentido de las latitudes, y se dice que la función es sectorial. Para otro casos, las funciones forman un damero sobre la esfera.

Ejemplos de los primeros armónicos esféricos

Expresiones analíticas de los primeros armónicos esféricos ortonormalizados, que usan la convención de fase de Condon-Shortley:

Y00(θ,φ)=121π{displaystyle Y_{0}^{0}(theta ,varphi )={1 over 2}{sqrt {1 over pi }}}

Y1−1(θ,φ)=1232πsin⁡θe−iφ{displaystyle Y_{1}^{-1}(theta ,varphi )={1 over 2}{sqrt {3 over 2pi }},sin theta ,e^{-ivarphi }}

Y10(θ,φ)=123πcos⁡θ{displaystyle Y_{1}^{0}(theta ,varphi )={1 over 2}{sqrt {3 over pi }},cos theta }

Y11(θ,φ)=−1232πsin⁡θeiφ{displaystyle Y_{1}^{1}(theta ,varphi )={-1 over 2}{sqrt {3 over 2pi }},sin theta ,e^{ivarphi }}

Y2−2(θ,φ)=14152πsin2⁡θe−2iφ{displaystyle Y_{2}^{-2}(theta ,varphi )={1 over 4}{sqrt {15 over 2pi }},sin ^{2}theta ,e^{-2ivarphi }}

Y2−1(θ,φ)=12152πsin⁡θcos⁡θe−iφ{displaystyle Y_{2}^{-1}(theta ,varphi )={1 over 2}{sqrt {15 over 2pi }},sin theta ,cos theta ,e^{-ivarphi }}

Y20(θ,φ)=145π(3cos2⁡θ−1){displaystyle Y_{2}^{0}(theta ,varphi )={1 over 4}{sqrt {5 over pi }},(3cos ^{2}theta -1)}

Y21(θ,φ)=−12152πsin⁡θcos⁡θeiφ{displaystyle Y_{2}^{1}(theta ,varphi )={-1 over 2}{sqrt {15 over 2pi }},sin theta ,cos theta ,e^{ivarphi }}

Y22(θ,φ)=14152πsin2⁡θe2iφ{displaystyle Y_{2}^{2}(theta ,varphi )={1 over 4}{sqrt {15 over 2pi }},sin ^{2}theta ,e^{2ivarphi }}

Y30(θ,φ)=147π(5cos3⁡θ−3cos⁡θ){displaystyle Y_{3}^{0}(theta ,varphi )={1 over 4}{sqrt {7 over pi }},(5cos ^{3}theta -3cos theta )}

Tabla de armónicos esféricos hasta Y₁₀

Generalizaciones

El mapa de los armónicos esféricos puede ser visto como representaciones de la simetría de grupo de rotaciones alrededor de un punto (SO(3)) y recubridor universal SU(2). Por lo tanto, capturan la simetría de la esfera de dos dimensiones. Cada grupo de armónicos esféricos con un valor dado del parámetro l da lugar a una representación irreductible diferente del grupo SO(3).

Además, la esfera es equivalente a la esfera de Riemann. El conjunto completo de simetrías de la esfera de Riemann se describen mediante el grupo de transformaciones de Möbius PSL(2,C), que es isomorfo al grupo de Lie real llamado grupo de Lorentz. El análogo de los armónicos esféricos con respecto al grupo de Lorentz es la serie hipergeométrica; de hecho, los armónicos esféricos pueden reescribirse en términos de la serie hipergeométrica, dado que SO(3) es un subgrupo de PSL(2,C).

Más específicamente, se puede generalizar a la serie hipergeométrica para describir las simetrías de cualquier espacio de simetría; en particular, la serie hipergeométrica puede ser desarrollada para todo grupo de Lie^[1]​^[2]​^[3]​^[4]​

Véase también

• Coeficientes de Clebsch-Gordan


• Función armónica


• Grupo de rotaciones


• Teoría de Sturm-Liouville

Referencias

Bibliografía

• A.R. Edmonds, Angular Momentum in Quantum Mechanics, (1957) Princeton University Press, ISBN 0-691-07912-9.


• E. U. Condon and G. H. Shortley, The Theory of Atomic Spectra, (1970) Cambridge at the University Press, ISBN 0-521-09209-4, See chapter 3.


• J.D. Jackson, Classical Electrodynamics, ISBN 0-471-30932-X
  


• Albert Messiah, Quantum Mechanics, volume II. (2000) Dover. ISBN 0-486-40924-4.


• D. A. Varshalovich, A. N. Moskalev, V. K. Khersonskii Quantum Theory of Angular Momentum,(1988) World Scientific Publishing Co., Singapore, ISBN 9971-5-0107-4
  

Enlaces externos

• 
  Weisstein, Eric W. «Spherical harmonics». En Weisstein, Eric W. MathWorld (en inglés). Wolfram Research. 
  


• Spherical Harmonic Models of Planetary Topography


• Spherical harmonics generator in OpenGL


• 
  General Solution to LaPlace's Equation in Spherical Harmonics (Spherical Harmonic Analysis). Solid Earth Geophysics.

Software

• SHTOOLS: Fortran 95 software archive


• HEALPIX: Fortran 90 and C++ software archive


• SpherePack: Fortran 77 software archive


• SpharmonicKit